【题目】如图1,在平面直角坐标系中,点![]() 为坐标原点,点
为坐标原点,点![]() 为第一象限内一点,点
为第一象限内一点,点![]() 在
在![]() 轴正半轴上,且
轴正半轴上,且![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)动点![]() 以每秒2个单位长度的速度,从点
以每秒2个单位长度的速度,从点![]() 出发,沿
出发,沿![]() 轴正半轴匀速运动,设点
轴正半轴匀速运动,设点![]() 的运动时间为
的运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,请用含有
,请用含有![]() 的式子表示
的式子表示![]() ,并直接写出
,并直接写出![]() 的取值范围;
的取值范围;
(3)如图2,在(2)的条件下,点![]() 坐标为
坐标为![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,在点
,在点![]() 的运动过程中,直线
的运动过程中,直线![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 是以
是以![]() 为腰的等腰直角三角形?若存在,求出点
为腰的等腰直角三角形?若存在,求出点![]() 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.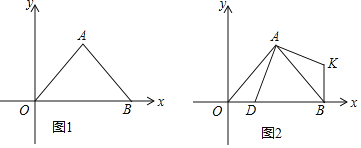
参考答案:
【答案】(1)(10,0);(2)S=25-5t(0<t≤5)或S=5t-25(t>5);(3)存在,(5,5)或(3,5)或(17,5).
【解析】
(1)作AM⊥OB于M,左侧△OAB是等腰直角三角形,得出∠OAB=90°,∠ABO=45°,BM=OM=5,求出OB=10,即可得出点B的坐标;
(2)分两种情况讨论:当0<t≤5时,OP=2t,则PB=10-2t;当t>5时,OP=2t,则PB=2t-10;由三角形面积公式即可得出结果;
(3)由ASA证明△OAD≌△BAK,得出OD=BK=2,分两种情况:当∠PRK=90°时,点R与A重合,得出R(5,5);当∠RPK=90°时,①当P在B的左侧时,作RE⊥OB于E,证得△EPR≌△BKP,得出EP=BK=2,RE=PB=5,求出OE=3即可;②当P在B的右侧时,同理得出点R的坐标为(17,5),即可得出结论.
(1)作AM⊥OB于M,如图1所示:
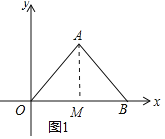
∵∠AOB=45°,OA=BA,点A(5,5),
∴△OAB是等腰直角三角形,∠OAB=90°,
∴∠ABO=45°,BM=OM=5,
∴OB=10,
∴点B的坐标为(10,0);
(2)当0<t≤5时,如图2所示:
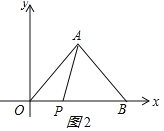
OP=2t,则PB=10-2t,
∴S=![]() (10-2t)×5=25-5t;
(10-2t)×5=25-5t;
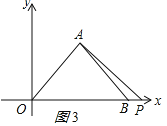
当t>5时,如图3所示:
OP=2t,则PB=2t-10,
∴S=![]() (2t-10)×5=5t-25;
(2t-10)×5=5t-25;
综上所述:S=25-5t(0<t≤5)或S=5t-25(t>5);
(3)存在,∵AK⊥AD,
∴∠DAK=90°=∠OAB,
∴∠OAD=∠BAK,
∵BK⊥OB,
∴∠ABK=90°-45°=45°,
在△OAD和△BAK中,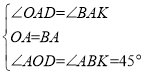 ,
,
∴△OAD≌△BAK(ASA),

∴OD=BK=2,
当∠PRK=90°时,点R与A重合,
∴R(5,5);
当∠RPK=90°时,
①当P在B的左侧时,如图4所示:
作RE⊥OB于E,同理证得△EPR≌△BKP,

∴EP=BK=2,RE=PB=5,
∴OE=10-5-2=3,
∴R(3,5);
②当P在B的右侧时,如图5所示:
同理得出点R的坐标为(17,5);
综上所述:直线a上存在点R,使△PKR是以PR为腰的等腰直角三角形,点R坐标为(5,5)或(3,5)或(17,5)./p>
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
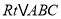 中,
中,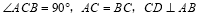 于点
于点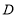 ,点
,点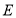 是射线
是射线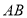 上一点,连接
上一点,连接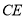 ,过点
,过点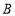 作
作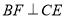 于点
于点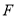 ,且交直线
,且交直线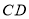 于点
于点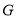 .
.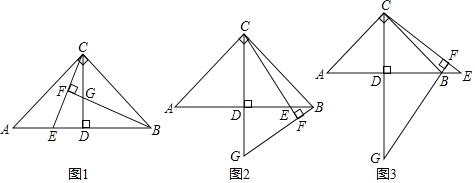
(1)如图1,当点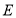 在线段
在线段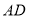 上时,求证:
上时,求证: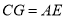 .
.
(2)如图2,当点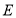 在线段
在线段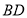 上时,其它条件不变,请猜想
上时,其它条件不变,请猜想 与
与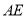 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(3)如图3,当点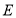 在线段
在线段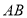 的延长线上时,其它条件不变,请直接写出
的延长线上时,其它条件不变,请直接写出 与
与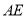 之间的数量关系.
之间的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学活动课上,小明提出这样一个问题:如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是_____.
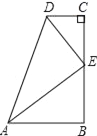
-
科目: 来源: 题型:
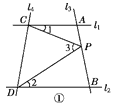
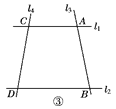
查看答案和解析>>【题目】如图①,已知直线l1∥l2,且l3和l1,l2分别相交于A,B两点,l4和l1,l2分别交于C,D两点,∠ACP=∠1,∠BDP=∠2,∠CPD=∠3,
点P在线段AB上.
(1)若∠1=22°,∠2=33°,则∠3=________;
(2)试找出∠1,∠2,∠3之间的等量关系,并说明理由;
(3)应用(2)中的结论解答下列问题;
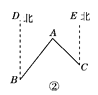
如图②,点A在B处北偏东40°的方向上,在C处的北偏西45°的方向上,求∠BAC的度数;
(4)如果点P在直线l3上且在A,B两点外侧运动时,其他条件不变,试探究∠1,∠2,∠3之间的关系(点P和A,B两点不重合),直接写出结论即可.
-
科目: 来源: 题型:
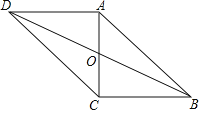
查看答案和解析>>【题目】如图,在ABCD中,对角线AC、BD交于点O,AC⊥BC,且ABCD的周长为36,△OCD的周长比△OBC的周长大2.
(1)求BC,CD的长;
(2)求ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一定范围内,弹簧的长度x(cm)与它所挂物体的重量y(g)之间满足关系式y=kx+b.已知挂重为50 g时,弹簧长12.5 cm;挂重为200 g时,弹簧长20 cm;那么当弹簧长15 cm时,挂重为( )
A. 80 g B. 100 g C. 120 g D. 150 g
相关试题

