【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M,N分别在AB,AD边上,若AM:MB=AN:ND=1:2,则sin∠MCN=( ) 
A.![]()
B.![]()
C.![]()
D.![]() ﹣2
﹣2
参考答案:
【答案】B
【解析】解:∵AB=AD=6,AM:MB=AN:ND=1:2, ∴AM=AN=2,BM=DN=4,
连接MN,连接AC,
∵AB⊥BC,AD⊥CD,∠BAD=60°
在Rt△ABC与Rt△ADC中,![]() ,
,
∴Rt△ABC≌Rt△ADC(HL),
∴∠BAC=∠DAC= ![]() ∠BAD=30°,MC=NC,
∠BAD=30°,MC=NC,
∴BC= ![]() AC,
AC,
∴AC2=BC2+AB2 , 即(2BC)2=BC2+AB2 ,
3BC2=AB2 ,
∴BC=2 ![]() ,
,
在Rt△BMC中,CM= ![]() =2
=2 ![]() ,
,
∵AN=AM,∠MAN=60°,
∴△MAN是等边三角形,
∴MN=AM=AN=2,
过M点作ME⊥CN于E,设NE=x,则CE=2 ![]() ﹣x,
﹣x,
∴MN2﹣NE2=MC2﹣EC2 , 即4﹣x2=(2 ![]() )2﹣(2
)2﹣(2 ![]() ﹣x)2 ,
﹣x)2 ,
解得:x= ![]() ,
,
∴EC=2 ![]() ﹣
﹣ ![]() =
= ![]() ,
,
由勾股定理得:ME= ![]() =
= ![]() =
= ![]() ,
,
∴sin∠MCN= ![]() =
= ![]() =
= ![]() ,
,
故选B.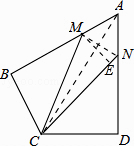
【考点精析】掌握相似三角形的判定与性质和解直角三角形是解答本题的根本,需要知道相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面一段:
计算
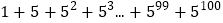
观察发现,上式从第二项起,每项都是它前面一项的
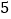 倍,如果将上式各项都乘以
倍,如果将上式各项都乘以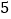 ,所得新算式中除个别项外,其余与原式中的项相同,于是两式相减将使差易于计算.
,所得新算式中除个别项外,其余与原式中的项相同,于是两式相减将使差易于计算.解:设
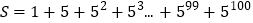 ,①
,①则
 ,②
,②②-①得
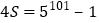 ,则
,则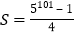 .
.上面计算用的方法称为“错位相减法”,如果一列数,从第二项起每一项与前一项之比都相等(本例中是都等于
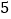 ),那么这列数的求和问题,均可用上述“错位相减”法来解决.
),那么这列数的求和问题,均可用上述“错位相减”法来解决.下面请你观察算式
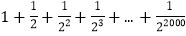 是否具备上述规律?若是,请你尝试用“错位相减”法计算上式的结果.
是否具备上述规律?若是,请你尝试用“错位相减”法计算上式的结果. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形的两条对角线的夹角为60°,如果一条对角线长为6,那么矩形的面积为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年十一黄金周期间,九寨沟7天中每天旅游人数的变化情况如下表(正数表示比9月30日多的人数,负数表示比9月30日少的人数):
日期
1日
2日
3日
4日
5日
6日
7日
人数变化/万人
+0.5
+0.7
+0.8

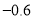
+0.2

(1)、请判断7天内游客人数量最多和最少的各是哪一天?它们相差多少万人?(5分)
(2)、如果9月30日旅游人数为2.5万人,平均每人消费500元,请问风景区在此7天内总收入为多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为体现社会对教师的尊重,教师节这天上午,出租车司机小王在东西走向的公路上免费接送老师.如果规定向东为正,向西为负,出租车的行程如下.(单位:千米)+15,﹣4,+13,﹣10,﹣12,+3,﹣13,﹣17
(1)当最后一名老师到达目的地时,小王距离开始接送第一位老师之前的地点的距离是多少?
(2)若出租车的耗油量为0.4升/千米,这天上午出租车共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为矩形纸片,把纸片ABCD折叠,使点B恰好落在CD边的中点E处, 折痕为AF,若CD=6,则AF等于__________.
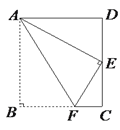
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆货车从仓库O出发在东西街道上运送水果,规定向东为正方向,一次到达的5个销售地点依次分别为A,B,C,D,E,最后回到仓库O,货车行驶的记录(单位:千米)如下:+1,+3,﹣6,﹣1,﹣2,+5.请问:
(1)请以仓库O为原点,向东为正方向,选择适当的单位长度,画出数轴,并标出A,B,C,D,E的位置;
(2)试求出该货车共行驶了多少千米?
(3)如果货车运送的水果以100千克为标准重量,超过的千克数记为正数,不足的千克数记为负数,则运往A,B,C,D,E五个地点的水果重量可记为:
+50,﹣15,+25,﹣10,﹣15,则该货车运送的水果总重量是多少千克?
相关试题

