搜索
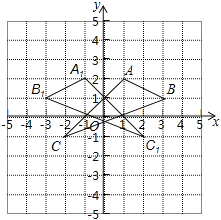
【题目】如图，在平面直角坐标系中，A(1，2)，B(3，1)，C(-2，-1).
（1）在图中作出
关于
轴对称的
.
（2）写出点
的坐标（直接写答案）.
A1_____________，B1______________，C1______________
参考答案：
【答案】（1）如图所示：
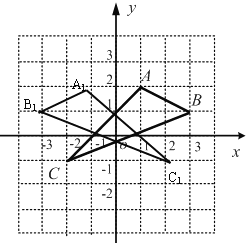
（2）A1（1，-2），B1（3，-1），C1（-2，1）
【解析】
（1）利用关于y轴对称点的性质得出对应点位置画出图形即可；（2）利用所画图形得出各点坐标；（3）利用△ABC所在矩形面积减去周围三角形面积进而求出即可．
本题解析：
(1)如图所示：
，即为所求；
(2)
(1,2)，
(3,1)，
(2,1)；
故答案为：(1,2),(3,1),(2,1)；
(3)的面积为：3×5
×2×1×3×3×2×5=4.5.故答案为：4.5.
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个自然数的立方，可以分裂成若干个连续奇数的和。例如：
和
分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和，即
=3+5；
=7+9+11； =13+15+17+19；…；若
也按照此规律来进行“分裂”，则“分裂”出的奇数中，最大的奇数是______.
-
科目： 来源： 题型：
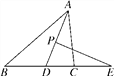
查看答案和解析>>【题目】如图，在△ABC中，AD平分∠BAC，P为线段AD上的一个动点，PE⊥AD交直线BC于点E，当P点在线段AD上运动时，∠E与∠B，∠ACB的数量关系为________________．
-
科目： 来源： 题型：
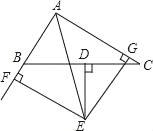
查看答案和解析>>【题目】如图，在△ABC中，BC边上的垂直平分线DE与∠BAC的平分线交于点E，EF⊥AB交AB的延长线于点F，EG⊥AC于点G．
求证：（1）BF＝CG；
（2）AB+AC＝2AF．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我们知道1+2+3+…+
=
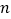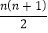，则1+2+3+…+10＝ ___________ .[问题提出] 那么
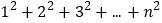的结果等于多少呢？[阅读理解] 在图1所示的三角形数阵中，第1行圆圈中的数为1，即12 ；第2行两个圆圈中数的和为2+2，即22；......；第n行n个圆圈中数的和为n+n+
n即 n2；这样，该三角形数阵中共有____ 个圆圈，所有圆圈中数的和可表示为_________________ .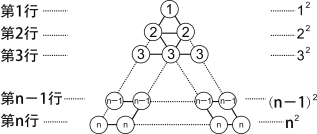 
图1
[规律探究] 将三角形数阵经两次旋转可得如图2所示的三角形数阵，观察这三个三角形数阵各行同一位置圆圈中的数（如第n－1行的第一个圆圈中的数分别为n－1，2，n）发现每个位置上三个圆圈中的数的和均为______________.由此可得，这三个三角形数阵所有圆圈中数的总和为：
3（
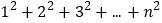）＝_________________.因此， ＝__________. 
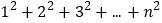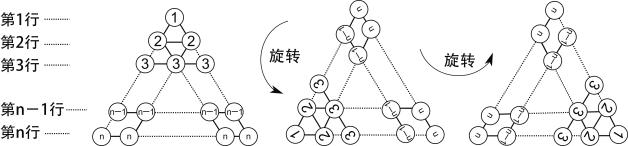
图2
[问题解决]
（1）.根据以上规律可得
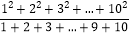__________________.（2）.试计算
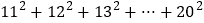，请写出计算步骤. -
科目： 来源： 题型：
查看答案和解析>>【题目】综合题。
（1）若一抛物线的顶点在原点，且经过点A（﹣2，8），求抛物线的解析式；
（2）如图，抛物线y=ax2+bx的顶点为A（﹣3，﹣3），且经过P（t，0）（t≠0），求该抛物线的解析式；
（3）在（2）的条件下，回答下列问题（直接写出答案） ①y的最小值为；
②点P的坐标为；
③当x＞﹣3时，y随x的增大而 ．
相关试题
