【题目】如图是市民广场到解百地下通道的手扶电梯示意图.其中AB、CD分别表示地下通道、市民广场电梯口处地面的水平线,∠ABC=135°,BC的长约是 ![]() m,则乘电梯从点B到点C上升的高度h是 m.
m,则乘电梯从点B到点C上升的高度h是 m.
参考答案:
【答案】5
【解析】解:过点C作AB的延长线的垂线CE,即乘电梯从点B到点C上升的高度h,
已知∠ABC=135°,
∴∠CBE=180°﹣∠ABC=45°,
∴CE=BCsin∠CBE=5 ![]() sin45°=5
sin45°=5 ![]()
![]() =5.
=5.
所以h=5,
所以答案是:5.
【考点精析】利用关于坡度坡角问题对题目进行判断即可得到答案,需要熟知坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AE切⊙O于点E,AT交⊙O于点M,N,线段OE交AT于点C,OB⊥AT于点B,已知∠EAT=30°,AE=3
 ,MN=2
,MN=2  .
.
(1)求∠COB的度数;
(2)求⊙O的半径R;
(3)点F在⊙O上( 是劣弧),且EF=5,把△OBC经过平移、旋转和相似变换后,使它的两个顶点分别与点E,F重合.在EF的同一侧,这样的三角形共有多少个?你能在其中找出另一个顶点在⊙O上的三角形吗?请在图中画出这个三角形,并求出这个三角形与△OBC的周长之比.
是劣弧),且EF=5,把△OBC经过平移、旋转和相似变换后,使它的两个顶点分别与点E,F重合.在EF的同一侧,这样的三角形共有多少个?你能在其中找出另一个顶点在⊙O上的三角形吗?请在图中画出这个三角形,并求出这个三角形与△OBC的周长之比. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE.下列结论中:
①CE=BD;
②△ADC是等腰直角三角形;
③∠ADB=∠AEB;
④CDAE=EFCG;
一定正确的结论有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】某市居民使用自来水按如下标准收费(水费按月缴纳):

(1)当a=2时,某用户一个月用了 28m3水,求该用户这个月应缴纳的水费;
(2)设某户月用水量为m立方米,当 m>20时,则该用户应缴纳的的水费为________元(用含 a、m的整式表示);
(3)当a=2时,甲、乙两用户一个月共用水 40m3,已知甲用户缴纳的水费超过了24元,设甲用户这个月用水xm3,试求甲、乙两用户一个月共缴纳的水费(用含 x的整式表示)。
-
科目: 来源: 题型:
查看答案和解析>>【题目】仔细阅读下面例题,然后按要求解答问题:
例题:已知二次三项式
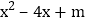 有一个因式是
有一个因式是 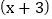 ,求另一个因式以及
,求另一个因式以及 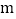 的值.
的值.解法一:设另一个因式为
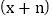 ,
,得
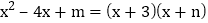 ,
,则
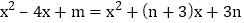 ,
,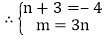 ,
,解得
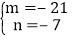 ,
, 另一个因式为
另一个因式为 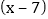 ,
,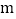 的值为
的值为 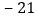 .
.解法二:∵二次三项式 x2-4x+m 有一个因式是 (x+3),
∴当x+3=0,即x=-3时,x2-4x+m=0.
把x=-3代入x2-4x+m=0,
得m=-21,
而x2-4x-21=(x+3)(x-7).
问题:分别仿照以上两种方法解答下面问题:
(1)已知二次三项式
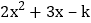 有一个因式是
有一个因式是 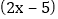 ,求另一个因式以及
,求另一个因式以及 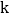 的值.
的值.解法一: 解法二:
(2)直接回答:
已知关于x的多项式 2x3
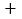 (3
(3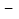 k)x2
k)x2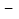 2x
2x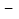 1有一个因式是
1有一个因式是 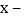 1,则k的值为_________.
1,则k的值为_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】先计算,再找出规律,然后根据规律进行计算.
(1)计算:①
 ②
② ③
③
(2)根据(1)中的计算,用字母表示出你发现的规律.
 =__________________
=__________________(3)根据(2)中的结论,计算下列结果:
①

②

③

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=﹣2x的图象与二次函数y=﹣x2+3x图象的对称轴交于点B.

(1)写出点B的坐标;
(2)已知点P是二次函数y=﹣x2+3x图象在y轴右侧部分上的一个动点,将直线y=﹣2x沿y轴向上平移,分别交x轴、y轴于C、D两点.若以CD为直角边的△PCD与△OCD相似,则点P的坐标为 .
相关试题

