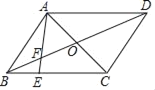
【题目】如图,在平行四边形ABCD中,AC,BD相交于点O,点E在BC上,AE交BD于F.
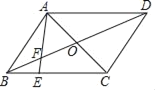
(1)若E是靠近点B的三等分点,求;①![]() 的值;②△BEF与△DAF的面积比;
的值;②△BEF与△DAF的面积比;
(2)当![]() 时,求
时,求![]() 的值.
的值.
参考答案:
【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]() .
.
【解析】
(1)①利用平行线分线段成比例定理即可解决问题;
②利用相似三角形的中面积比等于相似比的平方即可解决问题;
(2)利用平行四边形的性质可知OB=OD,BC∥AD,BC=AD,由题意![]() 可知BF:DF=n:(2m+n),即BE:AD=BF:DF=n:(2m+n),故求得
可知BF:DF=n:(2m+n),即BE:AD=BF:DF=n:(2m+n),故求得![]() =
=![]() .
.
解:(1)①∵四边形ABCD是平行四边形,
∴BC=AD,BC∥AD,
∵BE:BC=1:3,
∴![]() =
=![]() =
=![]() .
.
②∵BE∥AD,
∴△BEF∽△DAF,
∴![]() (
(![]() )2=
)2=![]() .
.
(2)∵四边形ABCD是平行四边形,
∴OB=OD,BC∥AD,BC=AD,
∵BF:OF=n:m,
∴BF:DF=n:(2m+n),
∴BE:AD=BF:DF=n:(2m+n),
∴![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我区实施课堂教学改革后,学生的自主学习、合作交流能力有很大提高,为了解学生自主学习、合作交流的具体情况,张老师对本班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
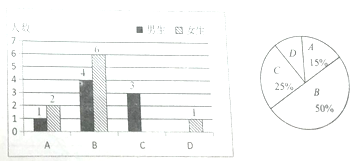
(1)本次调查中,张老师一共调查了_____名同学;
(2)将上面的条形统计图补充完整;
(3)为了共同进步,张老师从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一男一女的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一列货车从北京开往乌鲁木齐,以58km/h的平均速度行驶需要65h.为了实施西部大开发,京乌线决定全线提速.
(1)如果提速后平均速度为vkm/h,全程运营时间为t小时,试写出t与v之间的函数表达式;
(2)如果提速后平均速度为78km/h,求提速后全程运营时间;
(3)如果全程运营的时间控制在40h内,那么提速后,平均速度至少应为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=DC,E,F,G,H分别是AD,BC,BD,AC的中点.
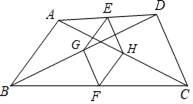
(1)证明:EG=EH;(2)证明:四边形EHFG是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
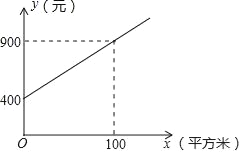
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)的关系如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,超过的部分每月每平方米加收4元.
(1)求如图所示的y与x的函数表达式;
(2)如果某学校目前的绿化面积是1200平方米.那么选择哪家公司的服务比较划算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的有( )
①用两颗钉子就可以把木条固定在墙上
②把笔尖看成一个点,当这个点运动时便得到一条线;
③把弯曲的公路改直,就能缩短路程;
④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上。
A.
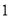 个B.
个B.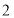 个C.
个C.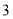 个D.
个D. 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数
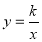 的图象经过点A(﹣1,a),过点A作AB⊥x轴,垂足为点B,△AOB的面积为
的图象经过点A(﹣1,a),过点A作AB⊥x轴,垂足为点B,△AOB的面积为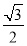 .
.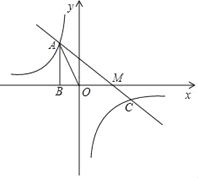
(1)求k的值;
(2)若一次函数y=mx+n图象经过点A和反比例函数图象上另一点
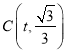 ,且与x轴交于M点,求AM的值;
,且与x轴交于M点,求AM的值;(3)在(2)的条件下,如果以线段AM为一边作等边△AMN,顶点N在另一个反比例函数
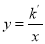 上,则k'= .
上,则k'= .
相关试题

