搜索
【题目】鹅岭公园内的小山坡上有一观景楼AB*（如图），山坡BC的坡度为i=1:2.4,为了测量观景楼AB的高度，小楚在山脚C处测得观景楼顶部A的仰角为45°，然后从山脚C沿山坡CB向上行走26米到达E处，测得观景楼顶部A的仰角为72°，（A、B、C、D、E在同一平面内），则观景楼AB的高度约为（ ）米.（结果精确到0.1米，参考数据： 
， 
， 
）
A. 15.6米 B. 18.1米 C. 19.2米 D. 22.5米
参考答案：
【答案】B
【解析】分析：如图，作EF⊥AD于F，作EG⊥CD于G， 
得到
用勾股定理
求出
根据
得到
根据AD=CD,列出方程求出
，利用
求出
即可求解.
详解：如图，作EF⊥AD于F，作EG⊥CD于G，
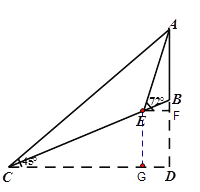
则EF=DG、FD=EG，
∵
即
解得： 
∴FD=EG=10，
设
由
知
∵
∴AD=CD,即
解得：x=7，
AD=CD=31，
解得： 
故选B.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，DE⊥AC于E，∠EDC:∠EDA=1:3 ，且AC=12，则DE的长度是（ ）
A. 3B. 6C.
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】元旦期间，某超市对出售
、
两种商品开展元旦促销活动，活动方案有如下两种：（同一种商品不可同时参与两种活动）商品
标价（单位：元）
方案一
每件商品出售价格
按标价降价
按标价降价
方案二
若所购商品超过
件（不同商品可累计）时，每件商品按标价降价
后出售（1）某单位购买
商品
件，商品
件，共花费
元，试求
的值；（2）在（1）求出的
值的条件下，若某单位购买
商品
件（为正整数），购买商品的件数比商品件数的
倍还多一件，请问该单位选择哪种方案才能获得最大优惠？请说明理由. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在边长为1的正方形ABCD中，动点E，F分别在边AB，CD上，将正方形ABCD沿直线EF折叠，使点B的对应点M始终落在边AD上（点M不与点A，D重合），点C落在点N处，MN与CD交于点P，设BE=x。
（1）当AM=
时，求x的值；（2）随着点M在边AD上位置的变化，ΔPDM的周长是否发生变化？如变化，请说明理由；如不变，请求出该定值；
（3）若AM=a,四边形BEFC的面积为S，求S与a之间的函数表达式。
-
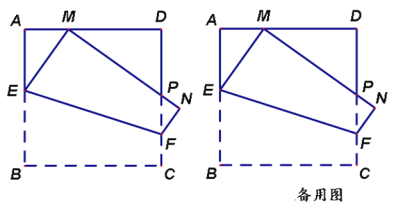
科目： 来源： 题型：
查看答案和解析>>【题目】如图,正方形ABCD的面积为12,△ABC是等边三角形,点E在正方形ABCD内,对角线AC上有一点P使PE+PD的和最小,这个最小值为( )
A.
B. 
C. 3 D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】春雨初歇，绿意葱茏，重庆南开（融侨）中学初2020级举行了“春天的赞礼”为主题的合唱比赛，各班演唱歌曲的曲风有：青春舞曲、经典名曲、动漫神曲、励志金曲四种类型，为了了解同学们对各种曲风的喜爱程度。校学生处对大众评委喜爱的歌曲曲风进行了调查，（A—喜爱青春舞曲、B—喜爱经典名曲、C—喜爱动漫神曲、D—喜爱励志金曲），先根据调查得到如下图不完整的统计图，请结合图中信息完成下列问题：
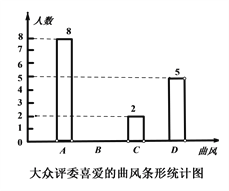
扇形统计图中“C—喜爱动漫神曲”对应扇形圆心角为【1】度，并补全条形统计图.
在此次比赛中，甲班演唱的《四季问候》和乙班演唱的《东方之珠》获得一等奖，《司机问候》由2名男生和2名女生领唱，《东方之珠》由1名男生和2名女生领唱，校学生处打算分别从这两首歌曲的领唱中任意选取1名同学参加校合唱团，请用画树状图或列表的方法求出恰好选到1名男生和1名女生的概率.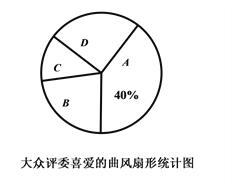
-
科目： 来源： 题型：
查看答案和解析>>【题目】数学兴趣小组研究某型号冷柜温度的变化情况，发现该冷柜的工作过程是：
当温度达到设定温度﹣20℃时，制冷停止，此后冷柜中的温度开始逐渐上升，当上升到﹣4℃时，制冷开始，温度开始逐渐下降，当冷柜自动制冷至一20℃时，制冷再次停止，．．
按照以上方式循环进行
同学们记录了44min 内15个时间点冷柜中的温度y（℃） 随时间x（min） 的变化情况，制成下表：
时间x/min
…
4
8
10
16
20
21
22
23
24
28
30
36
40
42
44
…
温度y/℃
…
﹣20
﹣10
﹣8
﹣5
﹣4
﹣8
﹣12
﹣16
﹣20
﹣10
﹣8
﹣5
﹣4
a
﹣20
…
（1）通过分析发现，冷柜中的温度y是时间x的函数．
①当4≤x＜20时，写出一个符合表中数据的函数解析式 ；
②当20≤x＜24时，写出一个符合表中数据的函数解析式 ；
（2）温度不低于﹣8℃的持续时间为 min；
（3）A的值为 ．
相关试题
