搜索
【题目】如图，在矩形ABCD中，DE⊥AC于E，∠EDC:∠EDA=1:3 ，且AC=12，则DE的长度是（ ）
A. 3B. 6C. 
D. 
参考答案：
【答案】D
【解析】
根据∠EDC：∠EDA=1：3，可得∠EDC=22.5°，∠EDA=67.5°，再由AC=12，求得DE．
解：∵四边形ABCD是矩形，
∴∠ADC=90°，AC=BD=12，OA=OC=
AC=6，OB=OD=BD=6，
∴OC=OD，
∴∠ODC=∠OCD，
∵∠EDC：∠EDA=1：3，∠EDC+∠EDA=90°，
∴∠EDC=22.5°，∠EDA=67.5°，
∵DE⊥AC，
∴∠DEC=90°，
∴∠DCE=90°-∠EDC=67.5°，
∴∠ODC=∠OCD=67.5°，
∵∠ODC+∠OCD+∠DOC=180°，
∴∠COD=45°，
∴OE=DE，
∵OE2+DE2=OD2，
∴2DE2=OD2=36，
∴DE=
，
故选：D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】由两个可以自由转动的转盘、每个转盘被分成如图所示的几个扇形、游戏者同时转动两个转盘，如果一个转盘转出了红色，另一转盘转出了蓝色，游戏者就配成了紫色下列说法正确的是（ ）
A. 两个转盘转出蓝色的概率一样大
B. 如果A转盘转出了蓝色，那么B转盘转出蓝色的可能性变小了
C. 先转动A 转盘再转动B 转盘和同时转动两个转盘，游戏者配成紫色的概率不同
D. 游戏者配成紫色的概率为
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球，它们除颜色外完全相同，其中红球有2 个，黄球有1个，蓝球有1个．现有一张电影票，小明和小亮决定通过摸球游戏定输赢，赢的一方得电影票．
（1）游戏规则1：两人各摸1个球，先由小明从纸箱里随机摸出1个球，记录颜色后放回，将小球摇匀，再由小亮随机摸出1个球．若两人摸到的球颜色相同，则小明赢，否则小亮赢．这个游戏规则对双方公平吗？请你利用树状图或列表法说明理由．
（2）游戏规则2； 两人同时各摸1个球，若两人摸到的球颜色相同，则小明赢，否则小亮赢．这个游戏小明赢得电影票的概率为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，平行四边形ABCD，DE⊥AB．垂足E在BA的延长线上，BF⊥DC，垂足F在DC的延长线上．
（1）求证：四边形BEDF是矩形；
（2）如图2，若M、N分别为AD、BC的中点，连接EM、EN、FM、FN，求证：四边形EMFN是平行四边形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】元旦期间，某超市对出售
、
两种商品开展元旦促销活动，活动方案有如下两种：（同一种商品不可同时参与两种活动）商品
标价（单位：元）
方案一
每件商品出售价格
按标价降价
按标价降价
方案二
若所购商品超过
件（不同商品可累计）时，每件商品按标价降价
后出售（1）某单位购买
商品
件，商品
件，共花费
元，试求
的值；（2）在（1）求出的
值的条件下，若某单位购买
商品
件（为正整数），购买商品的件数比商品件数的
倍还多一件，请问该单位选择哪种方案才能获得最大优惠？请说明理由. -
科目： 来源： 题型：
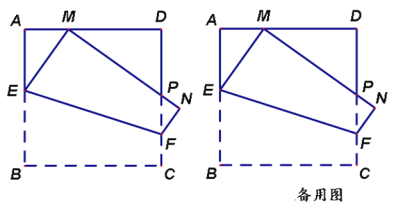
查看答案和解析>>【题目】如图，在边长为1的正方形ABCD中，动点E，F分别在边AB，CD上，将正方形ABCD沿直线EF折叠，使点B的对应点M始终落在边AD上（点M不与点A，D重合），点C落在点N处，MN与CD交于点P，设BE=x。
（1）当AM=
时，求x的值；（2）随着点M在边AD上位置的变化，ΔPDM的周长是否发生变化？如变化，请说明理由；如不变，请求出该定值；
（3）若AM=a,四边形BEFC的面积为S，求S与a之间的函数表达式。
-
科目： 来源： 题型：
查看答案和解析>>【题目】鹅岭公园内的小山坡上有一观景楼AB*（如图），山坡BC的坡度为i=1:2.4,为了测量观景楼AB的高度，小楚在山脚C处测得观景楼顶部A的仰角为45°，然后从山脚C沿山坡CB向上行走26米到达E处，测得观景楼顶部A的仰角为72°，（A、B、C、D、E在同一平面内），则观景楼AB的高度约为（ ）米.（结果精确到0.1米，参考数据：
， 
， 
）
A. 15.6米 B. 18.1米 C. 19.2米 D. 22.5米
相关试题
