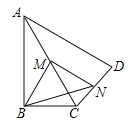
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)根据三角形中位线定理得MN=![]() AD,根据直角三角形斜边中线定理得BM=
AD,根据直角三角形斜边中线定理得BM=![]() AC,由此即可证明.
AC,由此即可证明.
(2)首先证明∠BMN=90°,根据![]() 即可解决问题.
即可解决问题.
试题解析:(1)证明:在△CAD中,∵M、N分别是AC、CD的中点,∴MN∥AD,MN=![]() AD,在RT△ABC中,∵M是AC中点,∴BM=
AD,在RT△ABC中,∵M是AC中点,∴BM=![]() AC,∵AC=AD,∴MN=BM.
AC,∵AC=AD,∴MN=BM.
(2)解:∵∠BAD=60°,AC平分∠BAD,∴∠BAC=∠DAC=30°,由(1)可知,BM=![]() AC=AM=MC,∴∠BMC=∠BAM+∠ABM=2∠BAM=60°,∵MN∥AD,∴∠NMC=∠DAC=30°,∴∠BMN=∠BMC+∠NMC=90°,∴
AC=AM=MC,∴∠BMC=∠BAM+∠ABM=2∠BAM=60°,∵MN∥AD,∴∠NMC=∠DAC=30°,∴∠BMN=∠BMC+∠NMC=90°,∴![]() ,由(1)可知MN=BM=
,由(1)可知MN=BM=![]() AC=1,∴BN=
AC=1,∴BN=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,已知A、B、C三点的坐标分别为A(﹣1,5),B(﹣3,0),C(﹣4,3).

(1)画出把△ABC向右平移6个单位,再向上平移1个单位长度的三角形A′B′C′;
(2)写出平移后三角形A′B′C′的各顶点的坐标;
(3)求三角形A′B′C′的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】把文字翻译成数学符号,构建方程组模型是解此类题的关键;方案型问题就是要构建双边不等式,有几个整数解就有几种方案;某工程队现有大量的沙石需要运输.工程队下属车队有载重量为8吨、10吨的卡车共12辆,全部车辆运输一次能运输110吨沙石.
(1)求该车队载重量为8吨、10吨的卡车各有多少辆?
(2)随着工程的进展,车队需要一次运输沙石165吨以上,为了完成任务,准备新增购这两种卡车共6辆,车队有多少种购买方案,请你一一写出. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个暗箱里放有a个除颜色外都完全相同的红、白、蓝三种球,其中红球有4个,白球有10个,每次将球搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球实验后发现,摸到红球的频率稳定在20%.
(1)试求出a的值;
(2)从中任意摸出一个球,下列事件:①该球是红球;②该球是白球;③该球是蓝球.试估计这三个事件发生的可能性的大小,并将三个事件按发生的可能性从小到大的顺序排列(用序号表示事件). -
科目: 来源: 题型:
查看答案和解析>>【题目】某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
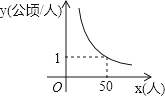
A.该村人均耕地面积随总人口的增多而增多
B.该村人均耕地面积y与总人口x成正比例
C.若该村人均耕地面积为2公顷,则总人口有100人
D.当该村总人口为50人时,人均耕地面积为1公顷 -
科目: 来源: 题型:
查看答案和解析>>【题目】某活动小组为了估计装有5个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共20组进行摸球实验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇总起来后,摸到红球次数为6000次.
(1)估计从袋中任意摸出一个球,恰好是红球的概率是多少?
(2)请你估计袋中红球接近多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:12﹣7×(﹣4)+8÷(﹣2)的结果是( )
A.﹣24
B.﹣20
C.6
D.36
相关试题

