【题目】如图所示,在平面直角坐标系中,已知A、B、C三点的坐标分别为A(﹣1,5),B(﹣3,0),C(﹣4,3).
(1)画出把△ABC向右平移6个单位,再向上平移1个单位长度的三角形A′B′C′;
(2)写出平移后三角形A′B′C′的各顶点的坐标;
(3)求三角形A′B′C′的面积.
参考答案:
【答案】
(1)解:△A′B′C′如图所示;

(2)解:A′(5,6),B′(3,1),C′(2,4)
(3)解:△A′B′C′的面积=3×5﹣ ![]() ×1×3﹣
×1×3﹣ ![]() ×2×5﹣
×2×5﹣ ![]() ×2×3,
×2×3,
=15﹣1.5﹣5﹣3,
=15﹣9.5,
=4.5
【解析】(1)根据点平移坐标变化规律:左减右加可求出;(3)斜三角形(三边都是倾斜无水平或竖直边)的面积基本求法是作差或求和.
【考点精析】掌握坐标与图形变化-平移是解答本题的根本,需要知道新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点;连接各组对应点的线段平行且相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一粒木质中国象棋棋子“車”,它的正面雕刻一个“車”字,它的反面是平的,将棋子从一定高度下抛,落地反弹后可能是“車”字面朝上,也可能是“車”字朝下.由于棋子的两面不均匀,为了估计“車”字朝上的机会,某实验小组做了棋子下抛实验,并把实验数据整理如下:
实验次数
20
40
60
80
100
120
140
160
“車”字朝上的频数
14
18
38
47
52
78
88
相应的频率
0.7
0.45
0.63
0.59
0.52
0.55
0.56
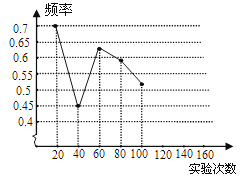
(1)请将表中数据补充完整,并画出折线统计图中剩余部分.
(2)如果实验继续进行下去,根据上表数据,这个实验的频率将接近于该事件发生的机会,请估计这个机会约是多少?
(3)在(2)的基础上,进一步估计:将该“車”字棋子,按照实验要求连续抛2次,则刚好使“車”字一次字面朝上,一次朝下的可能性为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解方程:x2﹣4x﹣5=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数
1
2
3
4
5
6
出现次数
8
10
7
9
16
10
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】把文字翻译成数学符号,构建方程组模型是解此类题的关键;方案型问题就是要构建双边不等式,有几个整数解就有几种方案;某工程队现有大量的沙石需要运输.工程队下属车队有载重量为8吨、10吨的卡车共12辆,全部车辆运输一次能运输110吨沙石.
(1)求该车队载重量为8吨、10吨的卡车各有多少辆?
(2)随着工程的进展,车队需要一次运输沙石165吨以上,为了完成任务,准备新增购这两种卡车共6辆,车队有多少种购买方案,请你一一写出. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个暗箱里放有a个除颜色外都完全相同的红、白、蓝三种球,其中红球有4个,白球有10个,每次将球搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球实验后发现,摸到红球的频率稳定在20%.
(1)试求出a的值;
(2)从中任意摸出一个球,下列事件:①该球是红球;②该球是白球;③该球是蓝球.试估计这三个事件发生的可能性的大小,并将三个事件按发生的可能性从小到大的顺序排列(用序号表示事件). -
科目: 来源: 题型:
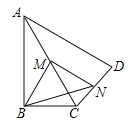
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
相关试题

