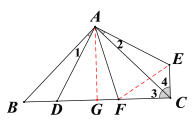
【题目】如图,在△ABC 中,∠BAC=90°,AB=AC,点D是BC上一动点,连接AD,过点A作AE⊥AD,并且始终保持AE=AD,连接CE.
(1)求证:△ABD ≌△ACE ;
(2)若AF平分∠DAE交BC于F,探究线段BD,DF,FC之间的数量关系,并证明;
(3)在(2)的条件下,若BD=3,CF=4,求AD的长.

参考答案:
【答案】(1)证明见解析;(2)BD2+FC2=DF2,理由见解析;(3)![]() .
.
【解析】
(1)根据垂直的定义以及直角,得到∠BAD=∠CAE,然后SAS证明即可;
(2)根据等腰直角三角形的性质得到∠B=∠ACB=45°,然后由(1)的结论得到∠ACE=45°,BD=CE,从而得到∠FCE=90°,根据勾股定理得出![]() ,再根据SAS证明△DAF≌△EAF,根据全等三角形的性质得到DF=FE,从而得到结论;
,再根据SAS证明△DAF≌△EAF,根据全等三角形的性质得到DF=FE,从而得到结论;
(3)过点A作![]() 于G,根据(2)的结论得到DF=5,然后根据等腰直角三角形的性质求出DG,最后根据勾股定理求解即可.
于G,根据(2)的结论得到DF=5,然后根据等腰直角三角形的性质求出DG,最后根据勾股定理求解即可.
(1)∵![]()
∴![]()
又∵![]()
∴![]()
在△ABD和△ACE中
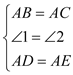
∴△ABD≌△ACE;
(2)![]() 理由如下:
理由如下:
连接FE, ∵![]()
∴![]()
由(1)知△ABD≌△ACE
∴![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∵AF平分![]()
∴![]()
在△DAF和△EAF中
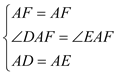
∴△DAF≌△EAF
∴![]() .
.
∴![]() ;
;
(3)过点A作![]() 于G
于G
由(2)知![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴在![]() 中
中![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E为对角线BD上一动点.若AB=
 ,当∠EAC=15°时,线段BE的长度为_________.
,当∠EAC=15°时,线段BE的长度为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】莫小贝在图1中画出△ABC,其顶点A,B,C都是格点,同时构造正方形BDEF,使它的顶点都在格点上,且它的边DE,EF分别经过点C,A,她借助此图求出了△ABC 的面积.
(1)莫小贝所画的△ABC 的三边长分别是AB=_______,BC=______,AC=______;△ABC 的面积为________.
(2)已知△ABC 中,AB=
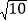 ,BC=
,BC=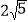 ,AC=
,AC=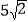 ,请你根据莫小贝的思路,在图2中画出△ABC ,并直接写出△ABC的面积_________.
,请你根据莫小贝的思路,在图2中画出△ABC ,并直接写出△ABC的面积_________.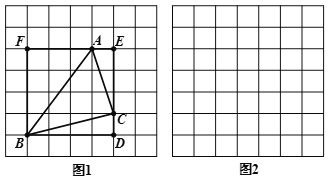
-
科目: 来源: 题型:
查看答案和解析>>【题目】在周长为26π的⊙O中,CD是⊙O的一条弦,AB是⊙O的切线,且AB∥CD,若AB和CD之间的距离为18,则弦CD的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平行四边形ABCD的顶点A在第三象限,对角线AC的中点在坐标原点,一边AB与x轴平行且AB=2,若点A的坐标为(a,b),则点D的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下四个命题:
①对应角和面积都相等的两个三角形全等;
②“若x2﹣x=0,则x=0”的逆命题;
③若关于x、y的方程组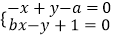 有无数多组解,则a=b=1;
有无数多组解,则a=b=1;
④将多项式5xy+3y﹣2x2y因式分解,其结果为﹣y(2x+1)(x﹣3).
其中正确的命题的序号为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)计算:( )﹣2+|
)﹣2+| 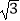 ﹣2|+3tan30°
﹣2|+3tan30°
(2)先化简,再求值: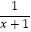 ﹣
﹣ 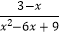 ÷
÷ 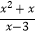 ,其中x=﹣
,其中x=﹣  .
.
相关试题

