搜索
【题目】计算
（1）计算：（ 
）﹣2+| 
﹣2|+3tan30°
（2）先化简，再求值： 
﹣ 
÷ 
，其中x=﹣ 
．
参考答案：
【答案】
（1）
解：原式=4+2﹣ 
+3× 
=6﹣ +
=6；
（2）
解：原式= 
﹣ 
= + 
= 
= 
，
当x=﹣ 
时，原式= 
=﹣ 
【解析】（1）分别根据负整数指数幂的计算法则、绝对值的性质及特殊角的三角函数值计算出各数，再根据实数混合运算的法则进行计算即可；
（2）先算除法，再算加减，最后把x的值代入进行计算即可．本题考查的是分式的化简求值，分式求值题中比较多的题型主要有三种：转化已知条件后整体代入求值；转化所求问题后将条件整体代入求值；既要转化条件，也要转化问题，然后再代入求值．
【考点精析】利用整数指数幂的运算性质和特殊角的三角函数值对题目进行判断即可得到答案，需要熟知aman=am+n(m、n是正整数)；（am）n=amn(m、n是正整数)；(ab)n=anbn(n是正整数)；am/an=am-n(a不等于0，m、n为正整数）；（a/b）n=an/bn(n为正整数)；分母口诀：30度、45度、60度的正弦值、余弦值的分母都是2，30度、45度、60度的正切值、余切值的分母都是3，分子口诀：“123，321，三九二十七”．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC 中，∠BAC=90°，AB=AC，点D是BC上一动点，连接AD，过点A作AE⊥AD，并且始终保持AE=AD，连接CE.
（1）求证：△ABD ≌△ACE ；
（2）若AF平分∠DAE交BC于F，探究线段BD，DF，FC之间的数量关系，并证明；
（3）在(2)的条件下，若BD=3，CF=4，求AD的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知平行四边形ABCD的顶点A在第三象限，对角线AC的中点在坐标原点，一边AB与x轴平行且AB=2，若点A的坐标为（a，b），则点D的坐标为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】以下四个命题：
①对应角和面积都相等的两个三角形全等；
②“若x2﹣x=0，则x=0”的逆命题；
③若关于x、y的方程组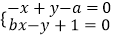
有无数多组解，则a=b=1；
④将多项式5xy+3y﹣2x2y因式分解，其结果为﹣y（2x+1）（x﹣3）．
其中正确的命题的序号为 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走为正，向下向左走为负.如果从A到B记为：A→B(+1，+4)，从B到A记为：B→A(-1，-4)，其中第一个数表示左右方向，第二个数表示上下方向．
（1）图中A→C( ， )，B→C( ， )，C→ (+1， )；
（2）若这只甲虫从A处去甲虫P处的行走路线依次为（+2，+2），（+2，-1），（-2，+3），（-1，-2），请在图中标出P的位置；
（3）若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程；
（4）若图中另有两个格点M、N，且M→A（3-a，b-4），M→N（5-a，b-2），则N→A应记为什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形OABC的边OA，OC分别与坐标轴重合，并且点B的坐标为
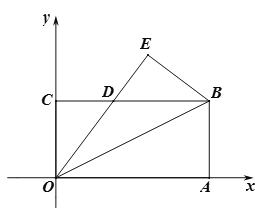
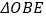.将该矩形沿OB折叠，使得点A落在点E处，OE与BC的交点为D.（1）求证：△OBD为等腰三角形；
（2）求点E的坐标；
（3）坐标平面内是否存在一点F，使得以点B，E，F，O为顶点的四边形是平行四边形，若存在，请直接写出点F的坐标；若不存在，请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】《算法统宗》是中国古代数学名著，作者是我国明代数学家程大位．在《算法统宗》中记载：“以绳测井，若将绳三折测之，绳多4尺，若将绳四折测之，绳多1尺，绳长井深各几何？”
译文：“用绳子测水井深度，如果将绳子折成三等份，井外余绳4尺；如果将绳子折成四等份，井外余绳1尺．问绳长、井深各是多少尺？”
设井深为x尺，根据题意列方程，正确的是（ ）
A. 3（x+4）=4（x+1） B. 3x+4=4x+1
C. 3（x﹣4）=4（x﹣1） D.
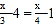
相关试题
