【题目】如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°,则∠BAC的度数为( )
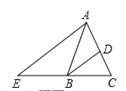
A. 40° B. 45° C. 60° D. 70°
参考答案:
【答案】A
【解析】根据平行线的性质可得∠CBD的度数,根据角平分线的性质可得∠CBA的度数,根据等腰三角形的性质可得∠C的度数,根据三角形内角和定理可得∠BAC的度数.
解:∵AE∥BD,∴∠CBD=∠E=35°,∵BD平分∠ABC,∴∠CBA=70°,∵AB=AC,
∴∠C=∠CBA=70°,∴∠BAC=180°﹣70°×2=40°.
故选A.
“点睛”考查了平行线的性质,角平分线的性质,等腰三角形的性质和三角形内角和定理.关键是得到∠C=∠CBA=70°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲有160元压岁钱,乙有200元压岁钱,要求甲给乙元压岁钱,才能使乙的压岁钱是甲压岁钱的2倍。
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(x2+nx+3)(x2﹣3x)的结果不含x3的项,那么n=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=-2x+6与坐标轴分别交于点A,B,正比例函数y=x的图象与直线y=-2x+6交于点C。

(1)求点A、B的坐标。
(2)求△BOC的面积
(3)已知点P是y轴上的一个动点,求BP+CP的最小值和此时点P的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,已知AB是⊙O直径,BC是⊙O的弦,弦ED⊥AB于点F,交BC于点G,过点C作⊙O的切线与ED的延长线交于点P.

(1)求证:PC=PG;
(2)点C在劣弧AD上运动时,其他条件不变,若点G是BC的中点,试探究CG、BF、BO三者之间的数量关系,并写出证明过程;
(3)在满足(2)的条件下,已知⊙O的半径为5,若点O到BC的距离为
 时,求弦ED的长.
时,求弦ED的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】到三角形的三个顶点距离相等的点是( )
A. 三条角平分线的交点
B. 三条边的垂直平分线的交点
C. 三条高的交点
D. 三条中线的交点
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动,设∠APB=y(单位:度),那么y与点P运动的时间x(单位:秒)的关系图是 ( )
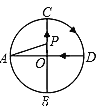
A.
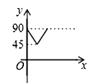 B.
B. 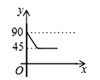 C.
C. 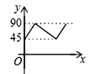 D.
D. 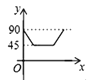
相关试题

