【题目】如图,点P1 , P2 , P3 , P4均在坐标轴上,且P1P2⊥P2P3 , P2P3⊥P3P4 , 若点P1 , P2的坐标分别为(0,﹣1),(﹣2,0),则点P4的坐标为 . 
参考答案:
【答案】(8,0)
【解析】解:∵点P1 , P2的坐标分别为(0,﹣1),(﹣2,0), ∴OP1=1,OP2=2,
∵Rt△P1OP2∽Rt△P2OP3 ,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得,OP3=4,
∵Rt△P2OP3∽Rt△P3OP4 ,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得,OP4=8,
则点P4的坐标为(8,0),
故答案为:(8,0).
根据相似三角形的性质求出P3D的坐标,再根据相似三角形的性质计算求出OP4的长,得到答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在双曲线y=
 上,点B在双曲线y=
上,点B在双曲线y=  (k≠0)上,AB∥x轴,分别过点A、B向x轴作垂线,垂足分别为D、C,若矩形ABCD的面积是8,则k的值为( )
(k≠0)上,AB∥x轴,分别过点A、B向x轴作垂线,垂足分别为D、C,若矩形ABCD的面积是8,则k的值为( )
A.12
B.10
C.8
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】一辆客车从甲地出发前往乙地,平均速度v(千米/小时)与所用时间t(小时)的函数关系如图所示,其中60≤v≤120.
(1)直接写出v与t的函数关系式;
(2)若一辆货车同时从乙地出发前往甲地,客车比货车平均每小时多行驶20千米,3小时后两车相遇.
①求两车的平均速度;
②甲、乙两地间有两个加油站A、B,它们相距200千米,当客车进入B加油站时,货车恰好进入A加油站(两车加油的时间忽略不计),求甲地与B加油站的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关系中,两个量之间为反比例函数关系的是( )
A.正方形的面积S与边长a的关系
B.正方形的周长l与边长a的关系
C.矩形的长为a , 宽为20,其面积S与a的关系
D.矩形的面积为40,长a与宽b之间的关系 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,AD为等腰直角△ABC的高,点A和点C分别在正方形DEFG的边DG和DE上,连接BG,AE.

(1)求证:BG=AE;
(2)将正方形DEFG绕点D旋转,当线段EG经过点A时,(如图②所示)
①求证:BG⊥GE;
②设DG与AB交于点M,若AG:AE=3:4,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,顶点为M的抛物线y=a(x+1)2﹣4分别与x轴相交于点A,B(点A在点B的右侧),与y轴相交于点C(0,﹣3).
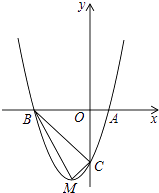
(1)求抛物线的函数表达式;
(2)判断△BCM是否为直角三角形,并说明理由.
(3)抛物线上是否存在点N(点N与点M不重合),使得以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等?若存在,求出点N的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)计算: +(1﹣
+(1﹣  )0﹣4cos45°.
)0﹣4cos45°.
(2)解方程组: .
.
相关试题

