【题目】计算下列各题
(1)计算: ![]() +(1﹣
+(1﹣ ![]() )0﹣4cos45°.
)0﹣4cos45°.
(2)解方程组: ![]() .
.
参考答案:
【答案】
(1)解:原式= ![]() +1﹣4×
+1﹣4× ![]() ,
,
=2 ![]() +1﹣2
+1﹣2 ![]() ,
,
=1.
(2)解:方程①×2+②得:3x=9,
方程两边同时除以3得:x=3,
将x=3代入①中得:3﹣y=2,
移项得:y=1.
∴方程组的解为 ![]()
【解析】(1)由a0=1以及特殊角的三角函数值,可得出(1﹣ ![]() )0=1,cos45°=
)0=1,cos45°= ![]() ,将其代入算式中即可得出结论;(2)根据用加减法解二元一次方程组的步骤解方程组即可得出结论.
,将其代入算式中即可得出结论;(2)根据用加减法解二元一次方程组的步骤解方程组即可得出结论.
【考点精析】根据题目的已知条件,利用零指数幂法则和解二元一次方程组的相关知识可以得到问题的答案,需要掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);二元一次方程组:①代入消元法;②加减消元法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P1 , P2 , P3 , P4均在坐标轴上,且P1P2⊥P2P3 , P2P3⊥P3P4 , 若点P1 , P2的坐标分别为(0,﹣1),(﹣2,0),则点P4的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,AD为等腰直角△ABC的高,点A和点C分别在正方形DEFG的边DG和DE上,连接BG,AE.

(1)求证:BG=AE;
(2)将正方形DEFG绕点D旋转,当线段EG经过点A时,(如图②所示)
①求证:BG⊥GE;
②设DG与AB交于点M,若AG:AE=3:4,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,顶点为M的抛物线y=a(x+1)2﹣4分别与x轴相交于点A,B(点A在点B的右侧),与y轴相交于点C(0,﹣3).
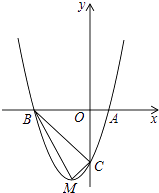
(1)求抛物线的函数表达式;
(2)判断△BCM是否为直角三角形,并说明理由.
(3)抛物线上是否存在点N(点N与点M不重合),使得以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等?若存在,求出点N的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校在落实国家“营养餐”工程中,选用了A,B,C,D种不同类型的套餐.实行一段时间后,学校决定在全校范围内随机抽取部分学生对“你喜欢的套餐类型(必选且只选一种)”进行问卷调查,将调查情况整理后,绘制成如图所示的两个统计图.

请你根据以上信息解答下列问题:
(1)在这次调查中,一共抽取了名学生;
(2)请补全条形统计图;
(3)如果全校有1200名学生,请你估计其中喜欢D套餐的学生的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一次测量活动中,小丽站在离树底部E处5m的B处仰望树顶C,仰角为30°,已知小丽的眼睛离地面的距离AB为1.65m,那么这棵树大约有多高?(结果精确到0.1m,参考数据:
 ≈1.73)
≈1.73)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与反比例函数y=
 的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C.
的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C. 
(1)求此反比例函数和一次函数的表达式;
(2)求点C的坐标及△AOB的面积.
相关试题

