【题目】完成下列推理说明:
如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.

证明:∵∠B+∠BCD=180°( ),
∴AB∥CD ( )
∴∠B= ( )
又∵∠B=∠D( 已知 ),
∴ ∠ = ∠ ( 等量代换 )
∴AD∥BE( )
∴∠E=∠DFE( )
参考答案:
【答案】详见解析
【解析】
根据平行线的判定得出AB∥CD,根据平行线的性质得出∠B=∠DCE,求出∠DCE=∠D,根据平行线的判定得出AD∥BE,根据平行线的性质得出即可.
证明:∵∠B+∠BCD=180°( 已知 ),
∴AB∥CD (同旁内角互补,两直线平行),
∴∠B= ∠DCE(两直线平行,同位角相等 ),
又∵∠B=∠D( 已知 ),
∴ ∠ DCE = ∠ D ( 等量代换 ),
∴AD∥BE(内错角相等,两直线平行),
∴∠E=∠DFE(两直线平行,内错角相等),
故答案为:同旁内角互补,两直线平行,∠DCE,两直线平行,同位角相等;∴∠DCE;∠D;内错角相等,两直线平行;两直线平行,内错角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入.下面是一周中每天的生产情况记录表(超过200辆记为正、不足200辆记为负):
星期
一
二
三
四
五
六
日
增减
+5
-2
-4
+13
-10
+16
-9
(1)根据记录可知前两天共生产 辆自行车;
(2)产量最多的一天比产量最少的一天多生产 辆自行车;
(3)该厂实行计件工资制,每生产一辆自行车可得80元.若超额完成任务,则超额部分每辆再奖20元;若没有完成计划工作量,则每少生产一辆扣20元,那么该厂工人这一周的工资总额是多少?
-
科目: 来源: 题型:
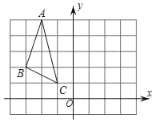
查看答案和解析>>【题目】如图,△ABC在平面直角坐标系中,A(﹣2,5),B(﹣3,2),C(﹣1,1).
(1)请画出△ABC关于y轴的对称图形△A′B′C′,其中A点的对应点是A′,B点的对应点是B′,C点的对应点是C′,并写出A′,B′,C′三点的坐标.
(2)求△A′B′C′的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B是数轴上的两个点,它们分别表示的数是
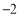 和1. 点A与点B之间的距离表示为AB.
和1. 点A与点B之间的距离表示为AB.(1)AB= .
(2)点P是数轴上A点右侧的一个动点,它表示的数是
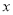 ,满足
,满足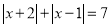 ,求
,求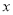 的值.
的值.(3)点C为6. 若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动.请问:
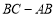 的值是否随着运动时间t(秒)的变化而改变? 若变化,请说明理由;若不变,请求其值.
的值是否随着运动时间t(秒)的变化而改变? 若变化,请说明理由;若不变,请求其值.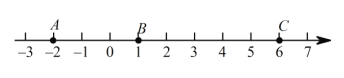
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD∥BC,∠EAD=∠C.

(1)试判断AE与CD的位置关系,并说明理由;
(2)若∠FEC=∠BAE,∠EFC=50°,求∠B的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着O﹣A﹣B﹣C﹣O的路线移动(即沿长方形移动一周).

(1)写出B点的坐标;
(2)当点P移动3秒时,求三角形OAP的面积;
(3)在移动过程中,当点P到x轴距离为4个单位长度时,求点P移动的时间.
-
科目: 来源: 题型:
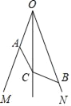
查看答案和解析>>【题目】如图,OC平分∠MON,A、B分别为OM、ON上的点,且BO>AO,AC=BC,求证:∠OAC+∠OBC=180°.
相关试题

