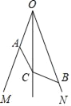
【题目】如图,OC平分∠MON,A、B分别为OM、ON上的点,且BO>AO,AC=BC,求证:∠OAC+∠OBC=180°.
参考答案:
【答案】见解析.
【解析】
如图,作CE⊥ON于E,CF⊥OM于F.由Rt△CFA≌Rt△CEB,推出∠ACF=∠ECB,推出∠ACB=∠ECF,由∠ECF+∠MON=360°﹣90°﹣90°=180°,可得∠ACB+∠AOB=180°,推出∠OAC+∠OBC=180°.
如图,作CE⊥ON于E,CF⊥OM于F.
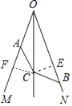
∵OC平分∠MON,CE⊥ON于E,CF⊥OM于F.
∴CE=CF,
∵AC=BC,∠CEB=∠CFA=90°,
∴Rt△CFA≌Rt△CEB(HL),
∴∠ACF=∠ECB,
∴∠ACB=∠ECF,
∵∠ECF+∠MON=360°﹣90°﹣90°=180°,
∴∠ACB+∠AOB=180°,
∴∠OAC+∠OBC=180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列推理说明:
如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.

证明:∵∠B+∠BCD=180°( ),
∴AB∥CD ( )
∴∠B= ( )
又∵∠B=∠D( 已知 ),
∴ ∠ = ∠ ( 等量代换 )
∴AD∥BE( )
∴∠E=∠DFE( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD∥BC,∠EAD=∠C.

(1)试判断AE与CD的位置关系,并说明理由;
(2)若∠FEC=∠BAE,∠EFC=50°,求∠B的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着O﹣A﹣B﹣C﹣O的路线移动(即沿长方形移动一周).

(1)写出B点的坐标;
(2)当点P移动3秒时,求三角形OAP的面积;
(3)在移动过程中,当点P到x轴距离为4个单位长度时,求点P移动的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列不等式(组)并把解集在数轴上表示出来
(1)2(2x﹣3)<5(x﹣1);
(2)1﹣
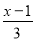 ≤
≤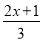 +x;
+x;(3)解不等式组
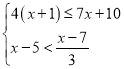 把解集在数轴上表示出来.
把解集在数轴上表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ΔABC中,以B为圆心,BC长为半径画弧,分别交AC、AB于D、E两点,并连接BD、DE.若∠A=30°,AB=AC,则∠BDE的度数为( )
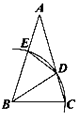
A.67.5°
B.52.5°
C.45°
D.75° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列三角形中,若AB=AC , 则能被一条直线分成两个小等腰三角形的是( )
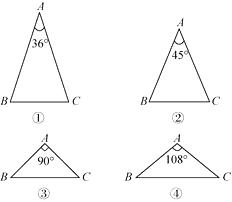
A.①②③
B.①②④
C.②③④
D.①③④
相关试题

