【题目】体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.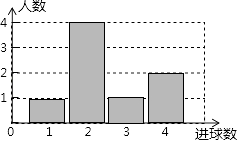
(1)求女生进球数的平均数、中位数;
(2)投球4次,进球3个以上(含3个)为优秀,全校有女生1200人,估计为“优秀”等级的女生约为多少人?
参考答案:
【答案】
(1)解:由条形统计图可得,女生进球数的平均数为:(1×1+2×4+1×3+4×2)÷8=2.5(个);
∵第4,5个数据都是2,则其平均数为:2;
∴女生进球数的中位数为:2
(2)解:样本中优秀率为: ![]() ,
,
故全校有女生1200人,“优秀”等级的女生为:1200× ![]() =450(人),
=450(人),
答:“优秀”等级的女生约为450人
【解析】(1)女生进球数的平均数为进球的总个数![]() 投球的人数;把8名女生进球的个数按从小到大的顺序排列出来,处于最中间位置的两个数的平均数就是中位数;
投球的人数;把8名女生进球的个数按从小到大的顺序排列出来,处于最中间位置的两个数的平均数就是中位数;
(2)这是一道用样本估计总体的题,首先找到样本优秀率为,然后用1200![]() 样本优秀率即可。
样本优秀率即可。
【考点精析】利用条形统计图和算术平均数对题目进行判断即可得到答案,需要熟知能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况;总数量÷总份数=平均数.解题关键是根据已知条件确定总数量以及与它相对应的总份数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5.OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
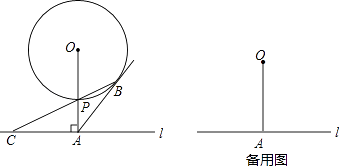
(1)试判断线段AB与AC的数量关系,并说明理由;
(2)若PC=2 ,求⊙O的半径和线段PB的长;
,求⊙O的半径和线段PB的长;
(3)若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,求⊙O的半径r的取值范围. -
科目: 来源: 题型:
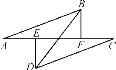
查看答案和解析>>【题目】如图,点A,E,F,C在一条直线上,若将△DEC的边EC沿AC方向平移,平移过程中始终满足下列条件:AE=CF,DE⊥AC于点E,BF⊥AC于点F,且AB=CD.则当点E,F不重合时,BD与EF的关系是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分8分)某厂制作甲、乙两种环保包装盒。已知同样用6m的材料制成甲盒的个数比制成乙盒的个数少2个,且制成一个甲盒比制作一个乙盒需要多用20%的材料。
(1)求制作每个甲盒、乙盒各用多少材料?
(2)如果制作甲、乙两种包装盒3000个,且甲盒的数量不少于乙盒数量的2倍,那么请写出所需材料总长度
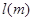 与甲盒数量
与甲盒数量 之间的函数关系式,并求出最少需要多少米材料。
之间的函数关系式,并求出最少需要多少米材料。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,下列条件中,能判断直线L1∥L2的是( )
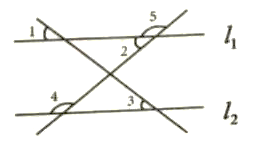
A. ∠2=∠3 B. ∠l=∠3 C. ∠4+∠5=180
 D. ∠2=∠4
D. ∠2=∠4 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级四个班在植树节这天义务植树
 一班植树x棵,二班植树的棵数比一班的2倍少40棵,三班植树的棵数比二班的一半多30棵,四班植树的棵数比三班的三分之一多50棵.
一班植树x棵,二班植树的棵数比一班的2倍少40棵,三班植树的棵数比二班的一半多30棵,四班植树的棵数比三班的三分之一多50棵. 求这四个班共植树多少棵
求这四个班共植树多少棵 用含x的代数式表示
用含x的代数式表示 ;
;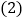 当
当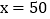 时,四个班哪个班植树最多?
时,四个班哪个班植树最多? 若四个班共植树266棵,一班植树多少棵.
若四个班共植树266棵,一班植树多少棵. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是用大小相同的小正方形拼成的图形,拼第1个图需要3个小正方形,拼第2个图需要8个小正方形,拼第3个图需要15个小正方形,
 .
. 根据拼图规律回答:第4个图形需要多少个小正方形;第n个图形比第
根据拼图规律回答:第4个图形需要多少个小正方形;第n个图形比第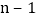 个图多需要多少个小正方形;第n个图形共需要多少个小正方形;
个图多需要多少个小正方形;第n个图形共需要多少个小正方形; 若第n个图形比第
若第n个图形比第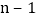 个多2019个小正方形,求n.
个多2019个小正方形,求n.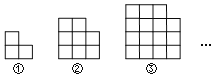
相关试题

