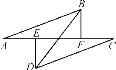
【题目】如图,点A,E,F,C在一条直线上,若将△DEC的边EC沿AC方向平移,平移过程中始终满足下列条件:AE=CF,DE⊥AC于点E,BF⊥AC于点F,且AB=CD.则当点E,F不重合时,BD与EF的关系是______.
参考答案:
【答案】互相平分
【解析】
由已知可推出AE+EF=CF+EF,DE⊥AC于E,BF⊥AC于F推出∠DEC=∠BFA=90°,AB=CD,所以推出△ABF≌△CDE,则DE=BF,所以证得△DOE≌△BOF,则得:OE=OF,OB=OD.
∵AE=CF, 点E,F不重合,
∴AE+EF=CF+EF,即AF=CE,
又∵DE⊥AC,BF⊥AC,
∴∠DEC=∠BFA=90°,
又∵AB=CD,
∴Rt△ABF≌Rt△CDE(HL),
∴DE=BF,
又∠DOE=∠BOF,
∴△DOE≌△BOF,
∴OE=OF,OB=OD,
∴BD和EF互相平分,
故答案为:互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在平面直角坐标系中,
 OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+b将
OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+b将 OABC的面积平分,则b=_______.
OABC的面积平分,则b=_______.(2)在平面直角坐标系中,直线y=2x+3关于原点对称的直线的表达式为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=﹣
 x+6的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.
x+6的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.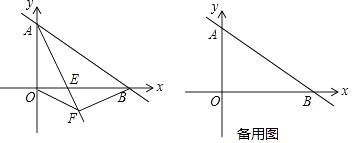
(1)求点B的坐标;
(2)求直线AE的表达式;
(3)过点B作BF⊥AE,垂足为F,连接OF,试判断△OFB的形状,并求△OFB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5.OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
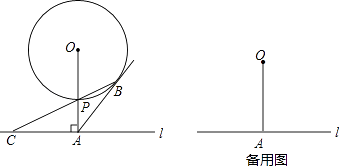
(1)试判断线段AB与AC的数量关系,并说明理由;
(2)若PC=2 ,求⊙O的半径和线段PB的长;
,求⊙O的半径和线段PB的长;
(3)若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,求⊙O的半径r的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分8分)某厂制作甲、乙两种环保包装盒。已知同样用6m的材料制成甲盒的个数比制成乙盒的个数少2个,且制成一个甲盒比制作一个乙盒需要多用20%的材料。
(1)求制作每个甲盒、乙盒各用多少材料?
(2)如果制作甲、乙两种包装盒3000个,且甲盒的数量不少于乙盒数量的2倍,那么请写出所需材料总长度
 与甲盒数量
与甲盒数量 之间的函数关系式,并求出最少需要多少米材料。
之间的函数关系式,并求出最少需要多少米材料。 -
科目: 来源: 题型:
查看答案和解析>>【题目】体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.
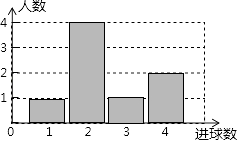
(1)求女生进球数的平均数、中位数;
(2)投球4次,进球3个以上(含3个)为优秀,全校有女生1200人,估计为“优秀”等级的女生约为多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,下列条件中,能判断直线L1∥L2的是( )
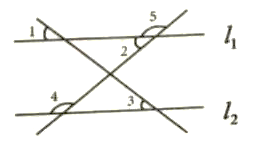
A. ∠2=∠3 B. ∠l=∠3 C. ∠4+∠5=180
 D. ∠2=∠4
D. ∠2=∠4
相关试题

