搜索
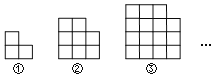
【题目】如图，是用大小相同的小正方形拼成的图形，拼第1个图需要3个小正方形，拼第2个图需要8个小正方形，拼第3个图需要15个小正方形，
．
根据拼图规律回答：第4个图形需要多少个小正方形；第n个图形比第
个图多需要多少个小正方形；第n个图形共需要多少个小正方形；
若第n个图形比第个多2019个小正方形，求n．
参考答案：
【答案】
15，
，
；
．
【解析】
第1个图形小正方形的个数为：
，第2个图形小正方形的个数为：
，第3个图形小正方形的个数为：
，
依此类推，第
个图形小正方形的个数为：
，第n个图形小正方形的个数为：
，第n个图形比第
个图多的小正方形的个数为：
，第n个图形比第个图多的小正方形的个数为：，即可得到答案，
结合的结果，得到关于n的一元一次方程，解之即可．
第1个图形小正方形的个数为：，
第2个图形小正方形的个数为：，
第3个图形小正方形的个数为：，
依此类推，
第个图形小正方形的个数为：，
第n个图形小正方形的个数为：，
第n个图形比第个图多的小正方形的个数为：，
故答案为：15，，，
根据题意得：
，
解得：．
-
科目： 来源： 题型：
查看答案和解析>>【题目】体育课上，老师为了解女学生定点投篮的情况，随机抽取8名女生进行每人4次定点投篮的测试，进球数的统计如图所示．
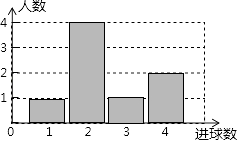
（1）求女生进球数的平均数、中位数；
（2）投球4次，进球3个以上（含3个）为优秀，全校有女生1200人，估计为“优秀”等级的女生约为多少人？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，下列条件中，能判断直线L1∥L2的是( )
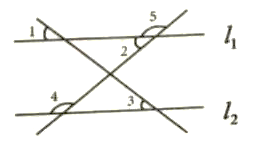
A. ∠2=∠3 B. ∠l=∠3 C. ∠4+∠5=180
D. ∠2=∠4 -
科目： 来源： 题型：
查看答案和解析>>【题目】某校七年级四个班在植树节这天义务植树
一班植树x棵，二班植树的棵数比一班的2倍少40棵，三班植树的棵数比二班的一半多30棵，四班植树的棵数比三班的三分之一多50棵．
求这四个班共植树多少棵
用含x的代数式表示
；
当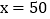
时，四个班哪个班植树最多？
若四个班共植树266棵，一班植树多少棵． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图,把直角梯形ABCD沿AD方向平移到梯形EFGH的位置,HG=24cm,MG=8cm,MC=6cm,则阴影部分的面积是____cm2.
-
科目： 来源： 题型：
查看答案和解析>>【题目】（本题8分）如图1，平行四边形ABCD中，点O是对角线AC的中点，EF过点O，与AD，BC分别相交于点E，F，GH过点O，与AB，CD分别相交于点G，H，连接EG，FG，FH，EH．
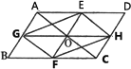
（1）求证：四边形EGFH是平行四边形；
（2）如图2，若EF//AB，GH//BC，在不添加任何辅助线的情况下，请直接写出图2中与四边形AGHD面积相等的所有平行四边形（四边形AGHD除外）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图①，已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
（2）如图②，将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
相关试题
