【题目】一个机器人从数轴原点出发,沿数轴正方向,以每前进3步后退2步的程序运动。设该机器人每秒钟前进或后退1步,并且每步的距离是1个单位长,![]() 表示第
表示第![]() 秒时机器人在数轴上的位置所对应的数。给出下列结论:①
秒时机器人在数轴上的位置所对应的数。给出下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 。其中,正确的结论的序号是( )
。其中,正确的结论的序号是( )
A.①③B.②③C.①②③D.①②④
参考答案:
【答案】D
【解析】
机器人每5秒完成一个循环,每个循环前进1步,n÷5的整数值即前进的步数,余数是1,总步数加1,是2加2,是3加3,是4加2.
解:依题意得:机器人每5秒完成一个前进和后退,即前5秒对应的数是1,2,3,2,1;
根据此规律即可推导判断:①和②,显然正确;
③中, 108÷5=21……3,故x108=21+3=24,104÷5=20……4,故x104=20+2=22,24>22,故错误;
④中,2018÷5=403……3,故x2018=403+3=406,2019÷5=÷5=403……4,故x2019=403+2=405,故正确.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)

(2)

(3)
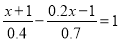
(4)
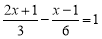
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在等边△ABC中,点D.E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
(1)求证:AD=CE
(2)求∠DFC的度数

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).

(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是
A. “明天降雨的概率是80%”表示明天有80%的时间都在降雨
B. “抛一枚硬币正面朝上的概率为
 ”表示每抛2次就有一次正面朝上
”表示每抛2次就有一次正面朝上C. “彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D. “抛一枚正方体骰子,朝上的点数为2的概率为
 ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在 附近
附近 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,抛物线y=ax2-6ax+6(a≠0)与x轴交于点A(8,0),与y轴交于点B,在X轴上有一动点E(m,0)(0<m<8),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
,抛物线y=ax2-6ax+6(a≠0)与x轴交于点A(8,0),与y轴交于点B,在X轴上有一动点E(m,0)(0<m<8),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.(
 )分别求出直线AB和抛物线的函数表达式;
)分别求出直线AB和抛物线的函数表达式;(
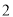 )设△PMN的面积为S1,△AEN的面积为S2,若S1:S2=36:25,求m的值;
)设△PMN的面积为S1,△AEN的面积为S2,若S1:S2=36:25,求m的值;(
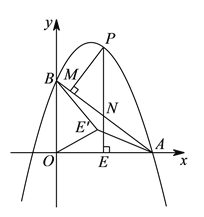
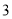 )如图2,在(
)如图2,在(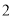 )条件下,将线段OE绕点O逆时针旋转得到OE',旋转角为α(0°<α<90°),连接E'A、E'B.
)条件下,将线段OE绕点O逆时针旋转得到OE',旋转角为α(0°<α<90°),连接E'A、E'B.①在x轴上找一点Q,使△OQE'∽△OE'A,并求出Q点的坐标;
②求BE'+
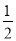 AE'的最小值.
AE'的最小值.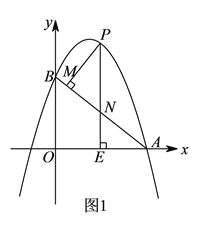
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
相关试题

