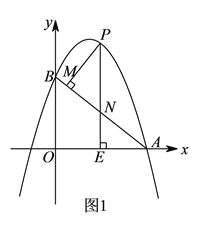
【题目】如图![]() ,抛物线y=ax2-6ax+6(a≠0)与x轴交于点A(8,0),与y轴交于点B,在X轴上有一动点E(m,0)(0<m<8),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
,抛物线y=ax2-6ax+6(a≠0)与x轴交于点A(8,0),与y轴交于点B,在X轴上有一动点E(m,0)(0<m<8),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
(![]() )分别求出直线AB和抛物线的函数表达式;
)分别求出直线AB和抛物线的函数表达式;
(![]() )设△PMN的面积为S1,△AEN的面积为S2,若S1:S2=36:25,求m的值;
)设△PMN的面积为S1,△AEN的面积为S2,若S1:S2=36:25,求m的值;
(![]() )如图2,在(
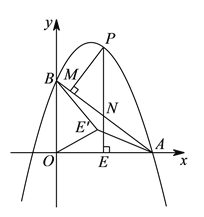
)如图2,在(![]() )条件下,将线段OE绕点O逆时针旋转得到OE',旋转角为α(0°<α<90°),连接E'A、E'B.
)条件下,将线段OE绕点O逆时针旋转得到OE',旋转角为α(0°<α<90°),连接E'A、E'B.
①在x轴上找一点Q,使△OQE'∽△OE'A,并求出Q点的坐标;
②求BE'+![]() AE'的最小值.
AE'的最小值.
参考答案:
【答案】(1)![]() ;
; ![]() ;(2)4;(3)①
;(2)4;(3)①![]() ,②
,②![]() .
.
【解析】分析:(1)把点A(8,0)代入抛物线y=ax-6ax+6,可求得a的值,从而可得到抛物线的解析式,然后求得点A和点B的坐标,最后利用待定系数法可求得直线AB的解析式;
(2)E(m,0),则N(m,-![]() m+6),P(m,
m+6),P(m, ![]() +6),然后证明△ANE∽△ABO,依据相似三角形的性质可求得AN的长,接下来,再证明△NMP∽△NEA,然后依据相似三角形的性质可得到
+6),然后证明△ANE∽△ABO,依据相似三角形的性质可求得AN的长,接下来,再证明△NMP∽△NEA,然后依据相似三角形的性质可得到![]() ,从而可求得PM=12-
,从而可求得PM=12-![]() m,然后依据PM=
m,然后依据PM=![]() m+3m,然后列出关于m的方程求解即可;
m+3m,然后列出关于m的方程求解即可;
(3)①在(2)的条件下,m=4,则OE′=OE=4,然后再证明△OQE′∽△OE′A,依据相似三角形的性质可得到![]() ,从而可求得OQ的值,于是可得到点Q的坐标;
,从而可求得OQ的值,于是可得到点Q的坐标;
②由①可知,当Q为(2,0)时,△OQE′∽△OE′A,且相似比为![]() ,于是得到BE′+
,于是得到BE′+![]() AE′=BE′+QE′,当点B、Q、E′在一条直线上时,BE′+QE′最小,最小值为BQ的长.
AE′=BE′+QE′,当点B、Q、E′在一条直线上时,BE′+QE′最小,最小值为BQ的长.
本题解析:
(![]() )把点
)把点![]() 代入抛物线
代入抛物线![]()
得![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() 与
与![]() 轴交点,令
轴交点,令![]() ,
,
得![]() ,
,
∴![]() .
.
设![]() 为
为![]() 过
过![]() ,
, ![]() ,
,
∴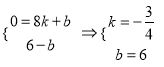 ,
,
∴![]() .
.
(![]() )∵过
)∵过![]() 作
作![]() 轴垂线交
轴垂线交![]() 于
于![]() ,交抛物线于
,交抛物线于![]() ,
,
∵![]() ,
,
∴![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴ ,
,
∴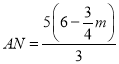 ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,∴
,∴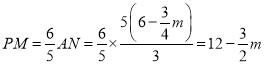 ,
,
∵![]() ,
,
∴![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() .
.
(![]() )①在(
)①在(![]() )的条件下,
)的条件下, ![]() ,∴
,∴![]() ,
,
设![]() ,∵旋转,∴
,∵旋转,∴![]() ,
,
若![]() ,
,
则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() .
.
②由①可知,当![]() 为
为![]() 时,
时,
![]() ,且相似比为
,且相似比为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴当![]() 旋转到
旋转到![]() 所在直线上时,
所在直线上时, ![]() 最小,即为
最小,即为![]() 长度,
长度,
∵![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() 的最小值为
的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).

(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个机器人从数轴原点出发,沿数轴正方向,以每前进3步后退2步的程序运动。设该机器人每秒钟前进或后退1步,并且每步的距离是1个单位长,
 表示第
表示第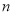 秒时机器人在数轴上的位置所对应的数。给出下列结论:①
秒时机器人在数轴上的位置所对应的数。给出下列结论:①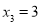 ;②
;②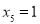 ;③
;③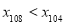 ;④
;④ 。其中,正确的结论的序号是( )
。其中,正确的结论的序号是( )A.①③B.②③C.①②③D.①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是
A. “明天降雨的概率是80%”表示明天有80%的时间都在降雨
B. “抛一枚硬币正面朝上的概率为
 ”表示每抛2次就有一次正面朝上
”表示每抛2次就有一次正面朝上C. “彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D. “抛一枚正方体骰子,朝上的点数为2的概率为
 ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在 附近
附近 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
-
科目: 来源: 题型:
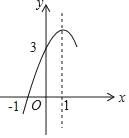
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③3a+c>0;
④当y>0时,x的取值范围是﹣1≤x<3;
⑤当x<0时,y随x增大而增大;
其中结论正确有_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=
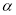 ,△BOC≌△ADC,∠OCD=60°,连接OD.
,△BOC≌△ADC,∠OCD=60°,连接OD.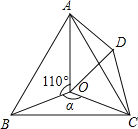
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试求证:△AOD是直角三角形;
(3)△AOD能否为等边三角形?为什么?
(4)探究:当α为多少度时,△AOD是等腰三角形.(直接写出答案)
相关试题

