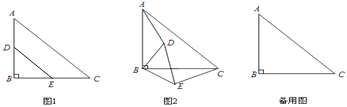
【题目】如图1,△DBE和△ABC都是等腰直角三角形,D,E两点分别在AB,BC上,∠B=90°.将△DBE绕点B顺时针旋转,得到图2.
(1)在图2中,求证:AD=CE;
(2)设AB= ![]() ,BD=
,BD= ![]() ,且当A、D、E三点在同一直线上时,∠EAC=30°,请利用备用图画出此情况下的图形,并求旋转的角度和
,且当A、D、E三点在同一直线上时,∠EAC=30°,请利用备用图画出此情况下的图形,并求旋转的角度和![]() 的值.
的值.
参考答案:
【答案】(1)详见解析;(2)30°,![]() .
.
【解析】试题分析:由△DBE和△ABC都是等腰直角三角形,可得AB=BC, DB=BE,∠ABD=∠CBE,根据“SAS”可证△ABD≌△CBE,从而AD=CE;
(2)先证△ABD≌△CBE,可求∠ADB=∠CEB=135°,可求∠AEC=90°,进而求出∠BAD=45°-30°=15°,根据三角形内角和即可旋转角∠ABD的度数;由AE=AD+DE=cos30 ·AC,整理可得![]() 的值.
的值.
解:(1)∵△DBE和△ABC都是等腰直角三角形,
∴AB=BC, DB=BE,∠ABC=∠DBE=90°,∴∠ABD=90°-∠DBC=∠CBE=90°-∠DBC,
∴△ABD≌△CBE,
∴AD=CE;
(2)如图, A、D、E三点在同一直线上时,

∵△DBE和△ABC都是等腰直角三角形,
∴∠BAC=∠BDE=∠BED =45°,
又△ABD≌△CBE,∴∠ADB=∠CEB=135°.
∴∠AEC=90°,
∵∠EAC=30°,
∴∠BAD=45°-30°=15°,∴∠ABD=30°,即旋转角为30°.
∵△DBE和△ABC是等腰直角三角形,AB=![]() , BD=
, BD=![]() ,
,
∴AC=![]() ,DE=
,DE=![]() ,
,
∵△ABD≌△CBE,
∴AD=EC,
∵∠EAC=30°,∠AEC=90°,AC= ![]() ,
,
∴AD=EC=![]() ,
,
∴AE=AD+DE=![]() +
+![]() =
=![]() ,
,
整理得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x1,x2,x3,…x2016都是不等于0的有理数,若y1=
 ,求y1的值.
,求y1的值.当x1>0时,y1=
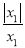 =
= =1;当x1<0时,y1=
=1;当x1<0时,y1= =
= =﹣1,所以y1=±1
=﹣1,所以y1=±1(1)若y2=
 +
+ ,求y2的值
,求y2的值(2)若y3=
 +
+ +
+ ,则y3的值为 ;
,则y3的值为 ;(3)由以上探究猜想,y2016=
 +
+ +
+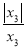 +…+
+…+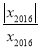 共有 个不同的值,在y2016这些不同的值中,最大的值和最小的值的差等于 .
共有 个不同的值,在y2016这些不同的值中,最大的值和最小的值的差等于 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(0,2),在x轴上取一点B,连接AB,以A为圆心,任意长为半径画弧,分别交OA、AB于点M、N,再以M、N为圆心,大于
 MN的长为半径画弧,两弧交于点D,连接AD并延长交x轴于点P.若△OPA与△OAB相似,则点P的坐标为( )
MN的长为半径画弧,两弧交于点D,连接AD并延长交x轴于点P.若△OPA与△OAB相似,则点P的坐标为( )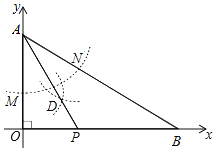
A. (1,0)B. (
 ,0)C. (
,0)C. (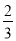
 ,0)D. (2
,0)D. (2 ,0)
,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径, BM切⊙O于点B,点P是⊙O上的一个动点(不经过A,B两点),过O作OQ∥AP交
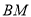 于点Q,过点P作
于点Q,过点P作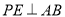 于C,交
于C,交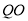 的延长线于点E,连结
的延长线于点E,连结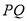 .
.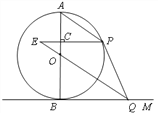
(1)求证:PQ与⊙O相切;
(2)若直径AB的长为12,PC=2EC,求tan∠E的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】蜗牛从某点O开始沿东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬行的各段路程依次为(单位:厘米):
 .问:
.问:(1)蜗牛最后是否回到出发点O?
(2)蜗牛离开出发点O最远是多少厘米?
(3)在爬行过程中,如果每爬行1厘米奖励一粒芝麻,则蜗牛可得到多少粒芝麻?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点A,B,C,D为直线l上从左到右顺次的4个点.

(1) ①直线l上以A,B,C,D为端点的线段共有 条;
②若AC=5cm,BD=6cm,BC=1cm,点P为直线l上一点,则PA+PD的最小值为 cm;(2)若点A在直线l上向左运动,线段BD在直线l上向右运动,M,N分别为AC,BD的中点(如图2),请指出在此过程中线段AD,BC,MN有何数量关系并说明理由;
(3)若C是AD的一个三等分点,DC>AC,且AD=9cm,E,F两点同时从C,D出发,分别以2cm/s,1cm/s的速度沿直线l向左运动,Q为EF的中点,设运动时间为t,当AQ+AE+AF=
 AD时,请直接写出t的值.
AD时,请直接写出t的值. -
科目: 来源: 题型:
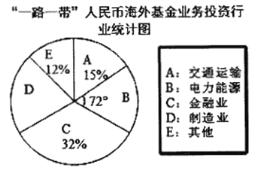
查看答案和解析>>【题目】“一路一带”倡议6岁了!到日前为止,中国已与126个国家和29个国际组织签署174份合作文件,共建“一路一带”国家已由亚欧延伸至非洲、拉美、南太等区域.截止2019年一季度末,人民币海外基金业务规模约3000亿元,其投资范围覆盖交通运输、电力能源、金融业和制造业等重要行业,投资行业统计图如图所示.
(1)求投资制造业的基金约为多少亿元?
(2)按照规划,中国将继续对“一路一带”基金增加投入,到2019年三季度末,共增加投入630亿元,假设平均每季度的增长率相等,求平均每季度的增长率是多少?
相关试题

