【题目】如图,在等边![]() 中,
中, ![]() 分别是边
分别是边![]() 上的点,且
上的点,且![]() ,
,![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 对称,连接
对称,连接![]() ,
,![]() 交
交![]() 于
于![]() .
.
(1)连接![]() ,则
,则![]() 之间的数量关系是 ;
之间的数量关系是 ;
(2)若![]() ,求
,求![]() 的大小(用
的大小(用![]() 的式子表示)
的式子表示)
(2)用等式表示线段![]() 和
和![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
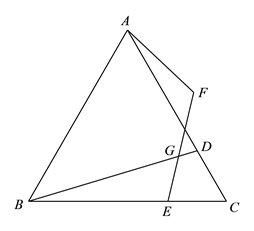
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() (3)
(3)![]() .
.
【解析】分析: (1)连接![]() ,
,![]() ,易证
,易证![]() 是等边三角形,则
是等边三角形,则![]() 根据点
根据点![]() 与点
与点![]() 关于
关于![]() 对称,则
对称,则![]() 根据等量代换可知
根据等量代换可知![]() ;
;
(2)根据![]() ,求出
,求出![]() .因为点
.因为点![]() 与点
与点![]() 关于
关于![]() 对称,得到
对称,得到![]() ,
,![]() .则
.则![]() .
.![]() ,
,![]() ,
,![]() 在以
在以![]() 为圆心,
为圆心,![]() 为半径的圆上.根据圆周角定理有
为半径的圆上.根据圆周角定理有![]() .
.
(3)![]() .理由如下:连接
.理由如下:连接![]() ,延长
,延长![]() ,
,![]() 交于点
交于点![]() ,证明
,证明![]() ,
,
得到![]() .根据
.根据![]() ,即可得到
,即可得到![]() .
.
(1)![]() ;
;
(2)如图:
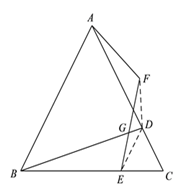
∵![]() 是等边三角形,
是等边三角形,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵点![]() 与点
与点![]() 关于
关于![]() 对称,
对称,
∴![]() ,
,![]() .
.
∴![]() .
.
由(1)知![]() .
.
∴![]() ,
,![]() ,
,![]() 在以
在以![]() 为圆心,
为圆心,![]() 为半径的圆上.
为半径的圆上.
∴![]() .
.
(3)![]() .理由如下:
.理由如下:
连接![]() ,延长
,延长![]() ,
,![]() 交于点
交于点![]() ,
,
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]() .
.
∵点![]() 与点
与点![]() 关于
关于![]() 对称,
对称,
∴![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
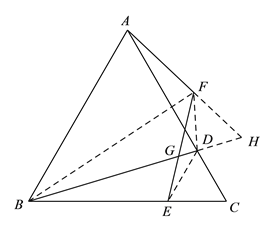
设![]() ,
,
则![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
由(2)知![]() .
.
∴![]() .
.
∴![]() ,
,![]() .
.
四边形![]() 中,
中,![]() .
.
∴![]() .
.
∴![]() 是等边三角形.
是等边三角形.
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 与
与![]() 中,
中,
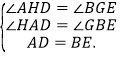
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
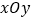 中,已知点
中,已知点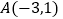 ,
,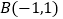 ,
,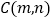 ,其中
,其中 ,以点
,以点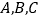 为顶点的平行四边形有三个,记第四个顶点分别为
为顶点的平行四边形有三个,记第四个顶点分别为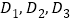 ,如图所示.
,如图所示.(1)若
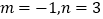 ,则点
,则点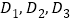 的坐标分别是( ),( ),( );
的坐标分别是( ),( ),( );(2)是否存在点
 ,使得点
,使得点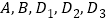 在同一条抛物线上?若存在,求出点
在同一条抛物线上?若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由. 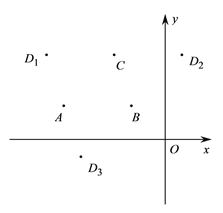
-
科目: 来源: 题型:
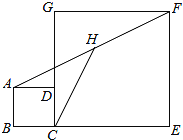
查看答案和解析>>【题目】如图,正方形ABCD和正方形CEFG中,点D在CG上,已知:BC=1,CE=7,H是AF的中点,则AF=_____,CH=_____.
-
科目: 来源: 题型:
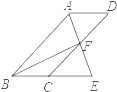
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】对某一个函数给出如下定义:若存在实数
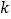 ,对于函数图象上横坐标之差为1的任意两点
,对于函数图象上横坐标之差为1的任意两点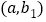 ,
,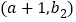 ,
,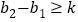 都成立,则称这个函数是限减函数,在所有满足条件的
都成立,则称这个函数是限减函数,在所有满足条件的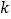 中,其最大值称为这个函数的限减系数.例如,函数
中,其最大值称为这个函数的限减系数.例如,函数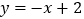 ,当
,当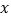 取值
取值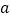 和
和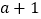 时,函数值分别为
时,函数值分别为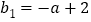 ,
,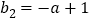 ,故
,故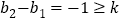 ,因此函数
,因此函数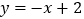 是限减函数,它的限减系数为
是限减函数,它的限减系数为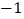 .
.(1)写出函数
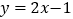 的限减系数;
的限减系数;(2)
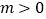 ,已知
,已知 (
(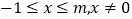 )是限减函数,且限减系数
)是限减函数,且限减系数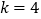 ,求
,求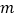 的取值范围.
的取值范围.(3)已知函数
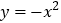 的图象上一点
的图象上一点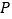 ,过点
,过点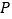 作直线
作直线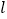 垂直于
垂直于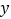 轴,将函数
轴,将函数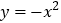 的图象在点
的图象在点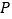 右侧的部分关于直线
右侧的部分关于直线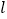 翻折,其余部分保持不变,得到一个新函数的图象,如果这个新函数是限减函数,且限减系数
翻折,其余部分保持不变,得到一个新函数的图象,如果这个新函数是限减函数,且限减系数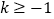 ,直接写出
,直接写出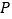 点横坐标
点横坐标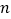 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形的顶点A(1,1),B(3,1),规定把等边△ABC“先沿x轴翻折,再向左平移1个单位”为一次变换,则一次变换后顶点C的坐标为____,如果这样连续经过2 017次变换后,等边△ABC的顶点C的坐标为____.

相关试题

