【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,以点
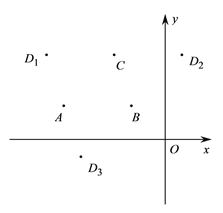
,以点![]() 为顶点的平行四边形有三个,记第四个顶点分别为
为顶点的平行四边形有三个,记第四个顶点分别为![]() ,如图所示.
,如图所示.
(1)若![]() ,则点
,则点![]() 的坐标分别是( ),( ),( );
的坐标分别是( ),( ),( );
(2)是否存在点![]() ,使得点
,使得点![]() 在同一条抛物线上?若存在,求出点
在同一条抛物线上?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
参考答案:
【答案】(1)![]() (-3,3),
(-3,3),![]() (1,3),
(1,3),![]() (-3,-1)(2)不存在
(-3,-1)(2)不存在
【解析】分析: (1)根据平行四边形对边相等的性质即可得到点![]() 的坐标.
的坐标.
(2)不存在. 假设满足条件的C点存在,即A,B,![]() ,
,![]() ,
,![]() 在同一条抛物线上,则线段AB的垂直平分线
在同一条抛物线上,则线段AB的垂直平分线![]() 即为这条抛物线的对称轴,而
即为这条抛物线的对称轴,而![]() ,
,![]() 在直线
在直线![]() 上,则
上,则![]()
![]() 的中点C也在抛物线对称轴上,故
的中点C也在抛物线对称轴上,故![]() ,即点C的坐标为(-2,n). 而
,即点C的坐标为(-2,n). 而![]() ,
,![]() 在直线
在直线![]() 上,则
上,则![]()
![]() 的中点C也在抛物线对称轴上,故
的中点C也在抛物线对称轴上,故![]() ,即点C的坐标为(-2,n).根据
,即点C的坐标为(-2,n).根据![]() 为抛物线的顶点.设出抛物线的方程,把点B的坐标代入得
为抛物线的顶点.设出抛物线的方程,把点B的坐标代入得![]() .把点
.把点![]() 的坐标代入得到
的坐标代入得到![]() ,与
,与![]() 矛盾. 所以不存在满足条件的C点.
矛盾. 所以不存在满足条件的C点.
(1)![]() (-3,3),
(-3,3),![]() (1,3),
(1,3),![]() (-3,-1)
(-3,-1)
(2)不存在. 理由如下:
假设满足条件的C点存在,即A,B,![]() ,
,![]() ,
,![]() 在同一条抛物线上,则线段AB的垂直平分线
在同一条抛物线上,则线段AB的垂直平分线![]() 即为这条抛物线的对称轴,而
即为这条抛物线的对称轴,而![]() ,
,![]() 在直线
在直线![]() 上,则
上,则![]()
![]() 的中点C也在抛物线对称轴上,故
的中点C也在抛物线对称轴上,故![]() ,即点C的坐标为(-2,n).
,即点C的坐标为(-2,n).
由题意得:![]() (-4,n),
(-4,n),![]() (0,n),
(0,n),![]() (-2,
(-2,![]() ).
).
注意到![]() 在抛物线的对称轴上,故
在抛物线的对称轴上,故![]() 为抛物线的顶点. 设抛物线的表达式是
为抛物线的顶点. 设抛物线的表达式是![]() .
.
当![]() 时,
时,![]() ,代入得
,代入得![]() .
.
所以![]() .
.
令![]() ,得
,得![]() ,解得
,解得![]() ,与
,与![]() 矛盾.
矛盾.
所以不存在满足条件的C点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连结BE分别交AC,AD于点F、G,连结OG,则下列结论:①OG=
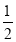 AB;②与△EGD全等的三角形共有5个;③S四边形ODGF>S△ABF;④由点A、B、D、E构成的四边形是菱形.其中正确的是( )
AB;②与△EGD全等的三角形共有5个;③S四边形ODGF>S△ABF;④由点A、B、D、E构成的四边形是菱形.其中正确的是( )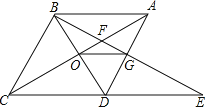
A.①④B.①③④C.①②③D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用三种大小不同的六个正方形和一个缺角的正方形拼成长方形
 ,其中
,其中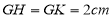 ,
,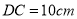 ,则长方形
,则长方形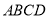 的面积为_____________.
的面积为_____________.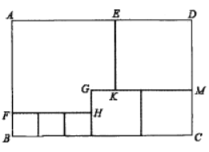
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知O为直线AD上一点,OB是∠AOC内部一条射线且满足∠AOB与∠AOC互补,OM,ON分别为∠AOC,∠AOB的平分线.
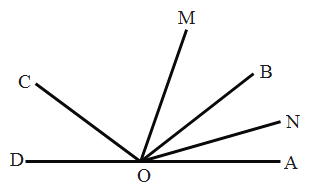
(1)∠COD与∠AOB相等吗?请说明理由;
(2)若∠AOB=30°,试求∠AOM与∠MON的度数;
(3)若∠MON=42°,试求∠AOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD和正方形CEFG中,点D在CG上,已知:BC=1,CE=7,H是AF的中点,则AF=_____,CH=_____.
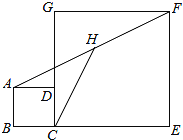
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.
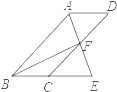
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边
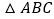 中,
中, 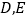 分别是边
分别是边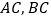 上的点,且
上的点,且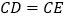 ,
,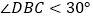 ,点
,点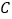 与点
与点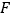 关于
关于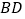 对称,连接
对称,连接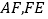 ,
, 交
交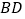 于
于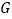 .
.(1)连接
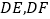 ,则
,则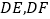 之间的数量关系是 ;
之间的数量关系是 ;(2)若
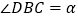 ,求
,求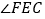 的大小(用
的大小(用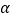 的式子表示)
的式子表示)(2)用等式表示线段
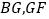 和
和 之间的数量关系,并证明.
之间的数量关系,并证明.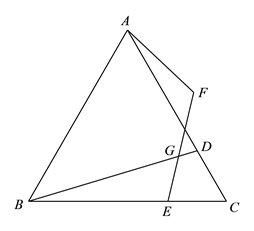
相关试题

