【题目】在正方形ABCD中,点E是AD的中点,连接BE,BF平分∠EBC交CD于点F,交AC于点G,将△CGF沿直线GF折叠至△C′GF,BD与△C′GF相交于点M、N,连接CN,若AB=6,则四边形CNC′G的面积是_____.

参考答案:
【答案】24![]() ﹣48
﹣48
【解析】
建立如图坐标系,延长BE交CD的延长线于K.则易知AB=DK=6,CK=12,BE=EK=3![]() ,BK=6
,BK=6![]() .利用角平分线的性质定理,求出CF,点G的坐标,再求出C′F的解析式,利用方程组求出点N的坐标,即可解决问题.
.利用角平分线的性质定理,求出CF,点G的坐标,再求出C′F的解析式,利用方程组求出点N的坐标,即可解决问题.
建立如图坐标系,延长BE交CD的延长线于K.则易知AB=DK=6,CK=12,BE=EK=3![]() ,BK=6
,BK=6![]() .
.

∵BF平分∠CBK,
∴![]() ,
,
CF=3(![]() 1),F[6,3(
1),F[6,3(![]() 1)].
1)].
∵CG平分∠ACF,
∴可得CG=9![]() 3
3![]() ,S△CGF=
,S△CGF=![]() CGCFsin45°=18
CGCFsin45°=18![]() 36,
36,
由C′(![]() ,
,![]() ),F[6,3(
),F[6,3(![]() -1)],
-1)],
∴直线C′F的解析式为y=![]() x+3
x+3![]() ,
,
由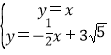 ,
,
解得N(2![]() ,2
,2![]() ),
),
∴S△CFN=![]() (62
(62![]() )3(
)3(![]() 1)=12
1)=12![]() 24,
24,
∴S四边形CNC′G=2S△CFGS△CFN=36![]() 7212
7212![]() +24=24
+24=24![]() 48.
48.
故答案为:24![]() 48.
48.
-
科目: 来源: 题型:
查看答案和解析>>【题目】课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图.
(1)求证:△ADC≌△CEB;
(2)从三角板的刻度可知AC=25cm,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相等).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A在第二象限,⊙A分别与x轴、y轴相切.若将⊙A向右平移5个单位,圆心A恰好落在直线y=2x﹣4上,则⊙A的半径为( )
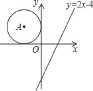
A.
 B. 2 C. 4 D. 6
B. 2 C. 4 D. 6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将直线y=x向下平移b个单位长度后得到直线l,l与反比例函数y=
 (k>0,x>0)的图象相交于点A,与x轴相交于点B,则OA2﹣OB2=10,则k的值是( )
(k>0,x>0)的图象相交于点A,与x轴相交于点B,则OA2﹣OB2=10,则k的值是( )
A. 5 B. 10 C. 15 D. 20
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕.若AB=3,BC=9.点D对应点是G.

(1)求BE长;
(2)求EF长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.将△ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C'顺时针旋转90°,得到△A″B″C′,
(1)请你画出△A′B′C′和△A″B″C′(不要求写画法).
(2)求出线段A′C′在旋转过程中所扫过的面积.(结果保留)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某校甲班学生外出去基地参观,乘车、行步、骑车的人数分布直方图和扇形统计图.
(1)根据统计图求甲班步行的人数;
(2)甲班步行的对象根据步行人数通过全班随机抽号来确定;乙班学生去基地分两段路走,即学校﹣﹣A地﹣﹣基地,每段路走法有乘车或步行或骑车,你认为哪个班的学生有步行的可能性少?(利用列表法或树状图求概率说明).

相关试题

