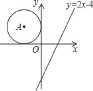
【题目】如图，在平面直角坐标系中，点A在第二象限，⊙A分别与x轴、y轴相切．若将⊙A向右平移5个单位，圆心A恰好落在直线y=2x﹣4上，则⊙A的半径为（　　）

A. B. 2 C. 4 D. 6

参考答案：

【答案】B

【解析】

由切线的性质可设A点的坐标为（a，a），再由平移可得到平移后的圆心坐标，代入直线解析式可求得a的值，可得出答案．

过A分别作x轴、y轴的垂线，垂足分别为E、F，如图，

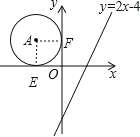
∵⊙A与x轴、y轴相切，

∴AE＝AF，

∵A在第二象限，

∴可设A点坐标为（a，a），

又A点向右平移5个单位，

∴A点平移后的坐标为（a＋5，a），

此时A点坐标在直线y＝2x4上，

∴a＝2（a＋5）4，解得a＝2，

∴AF＝2，即⊙A的半径为2，

故选：B．

关闭