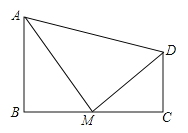
【题目】如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.
求证:(1)AM⊥DM;
(2)M为BC的中点.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据平行线的性质得到∠BAD+∠ADC=180°,根据角平分线的定义得到∠MAD+∠ADM=90°,根据垂直的定义得到答案;
(2)作NM⊥AD,根据角平分线的性质得到BM=MN,MN=CM,等量代换得到答案.
(1)∵AB∥CD,
∴∠BAD+∠ADC=180,
∵AM平分∠BAD,DM平分∠ADC,
∴2∠MAD+2∠ADM=180,
∴∠MAD+∠ADM=90,,
即AM⊥DM;
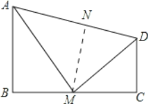
(2)作NM⊥AD交AD于N,
∵∠B=90,AB∥CD,
∴BM⊥AB,CM⊥CD,
∵AM平分∠BAD,DM平分∠ADC,
∴BM=MN,MN=CM,
∴BM=CM,
即M为BC的中点.
-
科目: 来源: 题型:
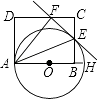
查看答案和解析>>【题目】如图,AH是⊙O的直径,矩形ABCD交⊙O于点E,连接AE,将矩形ABCD沿AE折叠,点B落在CD边上的点F处,画直线EF.
(1)求证:直线EF是⊙O的切线.
(2)若CD=10,EB=5,求⊙O的直径. -
科目: 来源: 题型:
查看答案和解析>>【题目】学生在操场上利用三角函数测量旗杆AB的高,直线l为水平地面,两个同学把30°的三角板和量角器按如图所示的方式垂直放在地面上,量角器的零刻度线与地面重合,此时旗杆顶部B的影子恰好落在三角形板的顶点D处和量角器37°的刻度C处,已知三角形板的边DE=60厘米,量角器的半径r=25厘米,量角器的圆心O到A的距离为5米.

(1)则∠AOC=°(直接写出答案)
(2)求旗杆AB的高度(精确到0.1米,参考数据sin37°≈0.6,cos37°≈0.8,tan37°≈0.75, ≈1.73)
≈1.73) -
科目: 来源: 题型:
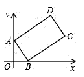
查看答案和解析>>【题目】如图,矩形ABCD中,AB=2,BC=4,点A、B分别在y轴、x轴的正半轴上,点C在第一象限,如果∠OAB=30°,那么点C的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将点A先向右平移3个单位长度,在向下平移5个单位长度,得到A’;将点B先向下平移5个单位长度,再向右平移4个单位长度,得到B’,则A’与B’相距( )

A. 4个单位长度 B. 5个单位长度 C. 6个单位长度 D. 7个单位长度
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按
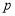 元/公里计算,耗时费按
元/公里计算,耗时费按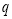 元/分钟计算(总费用不足
元/分钟计算(总费用不足 元按
元按 元计价).小敏、小刚两人用该打车方式出行,按上述计价规则,其行驶里程数、耗时以及打车总费用如下表:
元计价).小敏、小刚两人用该打车方式出行,按上述计价规则,其行驶里程数、耗时以及打车总费用如下表:里程数
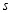 (公里)
(公里)耗时
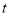 (分钟)
(分钟)车费(元)
小敏
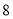
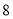

小刚
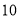

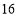
 求
求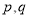 的值;
的值; 若小华也用该打车方式打车,平均车速为
若小华也用该打车方式打车,平均车速为 公里/时,行驶了
公里/时,行驶了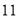
公里,那么小华的打车总费用为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明
如图,FG//CD,∠1=∠3,∠B=50°,求∠BDE的度数.
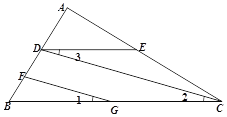
解:∵FG//CD (已知)
∴∠2=_________(____________________________)
又∵∠1=∠3,
∴∠3=∠2(等量代换)
∴BC//__________(_____________________________)
∴∠B+________=180°(______________________________)
又∵∠B=50°
∴∠BDE=________________.
相关试题

