【题目】如图,点D,E在△ABC的边BC上,连接AD,AE.下面有三个等式:①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,相构成以下三个命题:命题Ⅰ“如果①②成立,那么③成立”; 命题Ⅱ“如果①③成立,那么②成立”;命题Ⅲ“如果②③成立,那么①成立”. 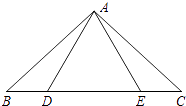
(1)以上三个命题是真命题的为(直接作答);
(2)请选择一个真命题进行证明(先写出所选命题,然后证明).
参考答案:
【答案】
(1)Ⅰ,Ⅱ,Ⅲ
(2)解:选择命题Ⅱ“如果①③成立,那么②成立”;
证明:∵AB=AC,
∴∠B=∠C,
在△ABD和△ACE中,
∵ 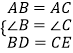
∴△ABD≌△ACE(SAS),
∴AD=AE.
【解析】解:(1)Ⅰ,Ⅱ,Ⅲ, 所以答案是:Ⅰ,Ⅱ,Ⅲ.
【考点精析】解答此题的关键在于理解命题与定理的相关知识,掌握我们把题设、结论正好相反的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题;经过证明被确认正确的命题叫做定理.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表,则方程ax2+bx+c=0的一个解的范围是( )
x
6.17
6.18
6.19
6.20
y
﹣0.03
﹣0.01
0.02
0.04
A.﹣0.01<x<0.02
B.6.17<x<6.18
C.6.18<x<6.19
D.6.19<x<6.20 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣2x+k=0的一个根是3,则另一个根是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD是⊙O的弦,AB是直径,且CD∥AB,连接AC、AD、OD,其中AC=CD,过点B的切线交CD的延长线于E.
(1)求证:DA平分∠CDO;
(2)若AB=12,求图中阴影部分的周长之和(参考数据:π=3.1,
 =1.4,
=1.4, =1.7).
=1.7).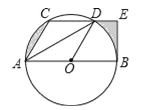
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=
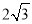 ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).
-
科目: 来源: 题型:
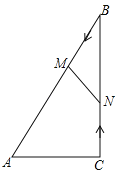
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5cm,∠BAC=60°,动点M从点B出发,在BA边上以每秒2cm的速度向点A匀速运动,同时动点N从点C出发,在CB边上以每秒
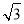 cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.
cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.(1)若BM=BN,求t的值;
(2)若△MBN与△ABC相似,求t的值;
(3)当t为何值时,四边形ACNM的面积最小?并求出最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=105°,∠DBC=75°.
(1)求证:BD=CD;
(2)若圆O的半径为3,求
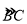 的长.
的长.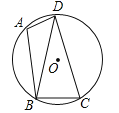
相关试题

