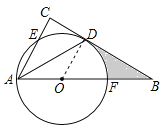
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=![]() ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).

参考答案:
【答案】(1)BC与⊙O相切;(2)![]() .
.
【解析】
试题分析:(1)连接OD,证明OD∥AC,即可证得∠ODB=90°,从而证得BC是圆的切线;
(2)在直角三角形OBD中,设OF=OD=x,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即为圆的半径,求出圆心角的度数,直角三角形ODB的面积减去扇形DOF面积即可确定出阴影部分面积.
试题解析:(1)BC与⊙O相切.
证明:连接OD.∵AD是∠BAC的平分线,∴∠BAD=∠CAD.又∵OD=OA,∴∠OAD=∠ODA,∴∠CAD=∠ODA,∴OD∥AC,∴∠ODB=∠C=90°,即OD⊥BC.又∵BC过半径OD的外端点D,∴BC与⊙O相切;
(2)设OF=OD=x,则OB=OF+BF=x+2,根据勾股定理得:![]() ,即
,即![]() ,解得:x=2,即OD=OF=2,∴OB=2+2=4,∵Rt△ODB中,OD=
,解得:x=2,即OD=OF=2,∴OB=2+2=4,∵Rt△ODB中,OD=![]() OB,∴∠B=30°,∴∠DOB=60°,∴S扇形AOB=
OB,∴∠B=30°,∴∠DOB=60°,∴S扇形AOB=![]() =
=![]() ,则阴影部分的面积为S△ODB﹣S扇形DOF=
,则阴影部分的面积为S△ODB﹣S扇形DOF=![]() =
=![]() .
.
故阴影部分的面积为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣2x+k=0的一个根是3,则另一个根是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD是⊙O的弦,AB是直径,且CD∥AB,连接AC、AD、OD,其中AC=CD,过点B的切线交CD的延长线于E.
(1)求证:DA平分∠CDO;
(2)若AB=12,求图中阴影部分的周长之和(参考数据:π=3.1,
 =1.4,
=1.4, =1.7).
=1.7).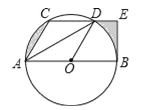
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D,E在△ABC的边BC上,连接AD,AE.下面有三个等式:①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,相构成以下三个命题:命题Ⅰ“如果①②成立,那么③成立”; 命题Ⅱ“如果①③成立,那么②成立”;命题Ⅲ“如果②③成立,那么①成立”.
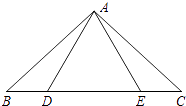
(1)以上三个命题是真命题的为(直接作答);
(2)请选择一个真命题进行证明(先写出所选命题,然后证明). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5cm,∠BAC=60°,动点M从点B出发,在BA边上以每秒2cm的速度向点A匀速运动,同时动点N从点C出发,在CB边上以每秒
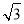 cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.
cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.(1)若BM=BN,求t的值;
(2)若△MBN与△ABC相似,求t的值;
(3)当t为何值时,四边形ACNM的面积最小?并求出最小值.
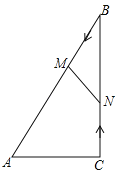
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=105°,∠DBC=75°.
(1)求证:BD=CD;
(2)若圆O的半径为3,求
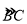 的长.
的长.
-
科目: 来源: 题型:
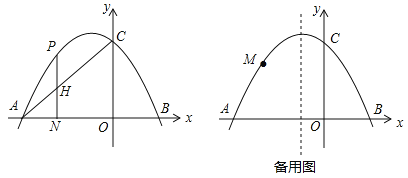
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
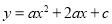 交x轴于A,B两点,交y轴于点C(0,3),tan∠OAC=
交x轴于A,B两点,交y轴于点C(0,3),tan∠OAC=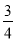 .
.(1)求抛物线的解析式;
(2)点H是线段AC上任意一点,过H作直线HN⊥x轴于点N,交抛物线于点P,求线段PH的最大值;
(3)点M是抛物线上任意一点,连接CM,以CM为边作正方形CMEF,是否存在点M使点E恰好落在对称轴上?若存在,请求出点M的坐标;若不存在,请说明理由.
相关试题

