【题目】如图,已知∠A=∠C,∠1+∠2=180°,试猜想AB与CD之间有怎样的位置关系?并说明理由.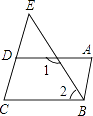
参考答案:
【答案】证明:AB∥CD,理由如下:
∵∠1+∠2=180°(已知)
∴AD∥BC(同旁内角互补,两直线平行)
∴∠EDA=∠C(两直线平行,同位角相等)
又∵∠A=∠C(已知)
∴∠A=∠EDA(等量代换)
∴AB∥CD.(内错角相等,两直线平行)
【解析】首先依据同旁内角互补,两直线平行可证明AD∥BC,然后依据平行线的性质可得到∠ADE=∠C,结合已知条件∠A=∠C,可得到∠ADE=∠A,最后,再依据内错角相等两直线平行线进行判断即可.
【考点精析】根据题目的已知条件,利用平行线的判定与性质的相关知识可以得到问题的答案,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2000度,全年用电量15万度.如果设上半年每月平均用电x度,则所列方程正确的是( )
A.6x+6(x-2000)=150000
B.6x+6(x+2000)=150000
C.6x+6(x-2000)=15
D.6x+6(x+2000)=15 -
科目: 来源: 题型:
查看答案和解析>>【题目】兰州市某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成家庭作业的时间不超过1.5小时,该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图(如图)的一部分.
时间(小时)
频数(人数)
频率
0≤t<0.5
4
0.1
0.5≤t<1
a
0.3
1≤t<1.5
10
0.25
1.5≤t<2
8
b
2≤t<2.5
6
0.15
合计
1

(1)在图表中,a= , b=;
(2)补全频数分布直方图;
(3)请估计该校1400名初中学生中,约有多少学生在1.5小时以内完成了家庭作业. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系,

(1)点A的坐标为 , 点C的坐标为 .
(2)将△ABC先向左平移3个单位长度,再向下平移6个单位长度,请画出平移后的△A1B1C1 .
(3)连接A1B,A1C,求△A1BC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】根据频数分布表或频数分布直方图求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数看作相应组中值的权,请你依据以上知识,解决下面的实际问题.
为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,并按载客量的多少分成A,B,C,D四组,得到如下统计图:

(1)求A组对应扇形圆心角的度数,并写出这天载客量的中位数所在的组;
(2)求这天5路公共汽车平均每班的载客量;
(3)如果一个月按30天计算,请估计5路公共汽车一个月的总载客量,并把结果用科学记数法表示出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的有( )
①对角线互相平分的四边形是平行四边形;
②平行四边形的对角互补;
③平行线间的线段相等;
④两个全等的三角形可以拼成一个平行四边形;
⑤平行四边形的四内角之比可以是2:3:2:3.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于分式
 ,总有( )
,总有( )
A.
B. (a≠-1)
(a≠-1)
C.
D.
相关试题

