【题目】已知:如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AF⊥BE于点F,那么线段BE,CE,AF三者之间的数量关系是 . 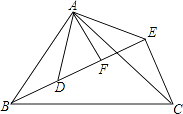
参考答案:
【答案】BE=CE+2AF
【解析】解:∵△ACB和△DAE均为等腰直角三角形, ∴AB=AC,AD=AE,∠BAC=∠DAE=90°,∠ADE=∠AED=45°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
在△ABD和△ACE中, ,
,
∴△ABD≌△ACE,
∴BD=CE,∠ADB=∠AEC,
∵点A,D,E在同一直线上,
∴∠ADB=180﹣45=135°,
∴∠AEC=135°,
∴∠BEC=∠AEC﹣∠AED=135﹣45=90°;
∵∠DAE=90°,AD=AE,AF⊥DE,
∴AF=DF=EF,
∴DE=DF+EF=2AF,
∴BE=BD+DE=CE+2AF.
所以答案是:BE=CE+2AF.
【考点精析】通过灵活运用等腰直角三角形,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明想了解全校3000名同学对新闻、体育、音乐、娱乐、戏曲五类电视节目的喜爱况,从中抽取了一部分同学进行了一次抽样调查,利用所得数据绘制成下面的统计图:根据图中所给信息,全校喜欢娱乐类节目的学生大约有( )人.
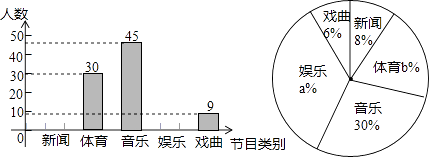
A.1080
B.900
C.600
D.108 -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式5x﹣12≤2(4x﹣3),并把它的解集在数轴上表示出来.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了测量出楼房AC的高度,从距离楼底C处
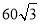 米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:
米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1: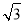 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈
的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈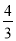 ,计算结果用根号表示,不取近似值).
,计算结果用根号表示,不取近似值).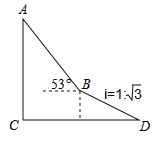
-
科目: 来源: 题型:
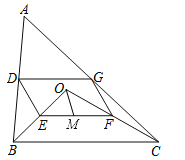
查看答案和解析>>【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于二次函数y=﹣2x2,下列结论正确的是( )
A.y随x的增大而增大B.图象关于直线x=0对称
C.图象开口向上D.无论x取何值,y的值总是负数
-
科目: 来源: 题型:
查看答案和解析>>【题目】若方程mx-2y=3x+4是关于x,y的二元一次方程,则m的取值范围是( )
A. m≠0 B. m≠3 C. m≠-3 D. m≠2
相关试题

