【题目】如图,为了测量出楼房AC的高度,从距离楼底C处![]() 米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:
米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:![]() 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈
的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈![]() ,计算结果用根号表示,不取近似值).
,计算结果用根号表示,不取近似值).
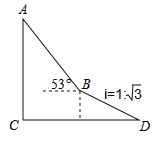
参考答案:
【答案】![]() .
.
【解析】
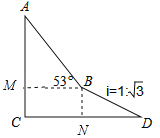
试题分析:如图作BN⊥CD于N,BM⊥AC于M,先在RT△BDN中求出线段BN,在RT△ABM中求出AM,再证明四边形CMBN是矩形,得CM=BN即可解决问题.
试题解析:如图作BN⊥CD于N,BM⊥AC于M.
在RT△BDN中,BD=30,BN:ND=1:![]() ,∴BN=15,DN=
,∴BN=15,DN=![]() ,∵∠C=∠CMB=∠CNB=90°,∴四边形CMBN是矩形,∴CM=BM=15,BM=CN=
,∵∠C=∠CMB=∠CNB=90°,∴四边形CMBN是矩形,∴CM=BM=15,BM=CN=![]() ,在RT△ABM中,tan∠ABM=
,在RT△ABM中,tan∠ABM=![]() ,∴AM=
,∴AM=![]() ,∴AC=AM+CM=
,∴AC=AM+CM=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对x,y定义了一种新运算T,规定T(x,y)=
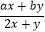 (其中a,b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=
(其中a,b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)= 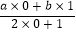 ,已知T(1,﹣1)=﹣2,T(4,2)=1.
,已知T(1,﹣1)=﹣2,T(4,2)=1.
(1)求a,b的值;
(2)若关于m的不等式组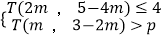 恰好有3个整数解,求p的取值范围.
恰好有3个整数解,求p的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明想了解全校3000名同学对新闻、体育、音乐、娱乐、戏曲五类电视节目的喜爱况,从中抽取了一部分同学进行了一次抽样调查,利用所得数据绘制成下面的统计图:根据图中所给信息,全校喜欢娱乐类节目的学生大约有( )人.
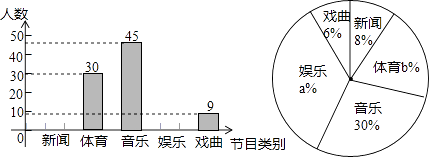
A.1080
B.900
C.600
D.108 -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式5x﹣12≤2(4x﹣3),并把它的解集在数轴上表示出来.

-
科目: 来源: 题型:
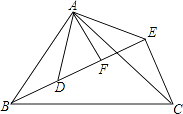
查看答案和解析>>【题目】已知:如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AF⊥BE于点F,那么线段BE,CE,AF三者之间的数量关系是 .
-
科目: 来源: 题型:
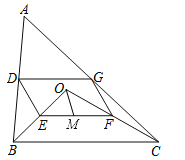
查看答案和解析>>【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于二次函数y=﹣2x2,下列结论正确的是( )
A.y随x的增大而增大B.图象关于直线x=0对称
C.图象开口向上D.无论x取何值,y的值总是负数
相关试题

