【题目】如图,直线y= ![]() x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )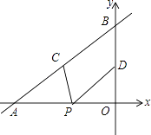
A.(﹣3,0)
B.(﹣6,0)
C.(﹣ ![]() ,0)
,0)
D.(﹣ ![]() ,0)
,0)
参考答案:
【答案】C
【解析】解:(方法一)作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,如图所示.
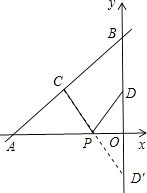
令y= ![]() x+4中x=0,则y=4,
x+4中x=0,则y=4,
∴点B的坐标为(0,4);
令y= ![]() x+4中y=0,则
x+4中y=0,则 ![]() x+4=0,解得:x=﹣6,
x+4=0,解得:x=﹣6,
∴点A的坐标为(﹣6,0).
∵点C、D分别为线段AB、OB的中点,
∴点C(﹣3,2),点D(0,2).
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,﹣2).
设直线CD′的解析式为y=kx+b,
∵直线CD′过点C(﹣3,2),D′(0,﹣2),
∴有 ![]() ,解得:
,解得: 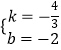 ,
,
∴直线CD′的解析式为y=﹣ ![]() x﹣2.
x﹣2.
令y=﹣ ![]() x﹣2中y=0,则0=﹣
x﹣2中y=0,则0=﹣ ![]() x﹣2,解得:x=﹣
x﹣2,解得:x=﹣ ![]() ,
,
∴点P的坐标为(﹣ ![]() ,0).
,0).
故选C.
(方法二)连接CD,作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,如图所示.
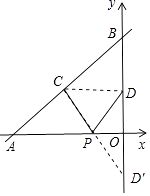
令y= ![]() x+4中x=0,则y=4,
x+4中x=0,则y=4,
∴点B的坐标为(0,4);
令y= ![]() x+4中y=0,则
x+4中y=0,则 ![]() x+4=0,解得:x=﹣6,
x+4=0,解得:x=﹣6,
∴点A的坐标为(﹣6,0).
∵点C、D分别为线段AB、OB的中点,
∴点C(﹣3,2),点D(0,2),CD∥x轴,
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,﹣2),点O为线段DD′的中点.
又∵OP∥CD,
∴点P为线段CD′的中点,
∴点P的坐标为(﹣ ![]() ,0).
,0).
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EHEA;
(3)若⊙O的直径为5,sinA=
 ,求BH的长.
,求BH的长.
-
科目: 来源: 题型:
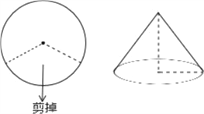
查看答案和解析>>【题目】如图,若将半径为6cm的圆形纸片剪去三分之一,剩下的部分围成一个圆锥的侧面,则围成圆锥的全面积为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长是2,点E是射线AB上一动点(点E与点A、B不重合),过点E作FG⊥DE交射线CB于点F、交DA的延长线于点G.
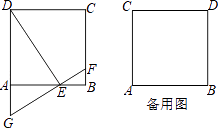
(1)求证:DE=GF.
(2)连结DF,设AE=x,△DFG的面积为y,求y与x之间的函数解析式.
(3)当Rt△AEG有一个角为30°时,求线段AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】国家体育馆“鸟巢”的建筑面积达25.8万平方米,请将“25.8万”用科学记数法表示,结果是( )
A.25.8×104B.25.8×105C.2.58×104D.2.58×105
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】要了解某地区八年级学生的身高情况,从中随机抽取150名学生的身高作为一个样本,身高均在141cm~175cm之间(取整数厘米),整理后分成7组,绘制出频数分布直方图(不完整).根据图中提供的信息,解答下列问题:
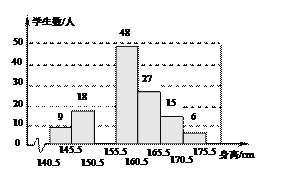
(1) 补全频数分布直方图;
(2) 抽取的样本中,学生身高的中位数在哪个小组?
(3) 该地区共有3 000名八年级学生,估计其中身高不低于161cm的人数.
相关试题

