【题目】已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EHEA;
(3)若⊙O的直径为5,sinA=![]() ,求BH的长.
,求BH的长.

参考答案:
【答案】(1)证明见试题解析;(2)证明见试题解析;(3)![]() .
.
【解析】试题分析:(1)由圆周角定理和已知条件证出∠ODB=∠ABC,再证出∠ABC+∠DBF=90°,即∠OBD=90°,即可得出BD是⊙O的切线;
(2)连接AC,由垂径定理得出![]() ,得出∠CAE=∠ECB,再由公共角∠CEA=∠HEC,证明△CEH∽△AEC,得出对应边成比例
,得出∠CAE=∠ECB,再由公共角∠CEA=∠HEC,证明△CEH∽△AEC,得出对应边成比例![]() ,即可得出结论;
,即可得出结论;
(3)连接BE,由圆周角定理得出∠AEB=90°,由三角函数求出BE,再根据勾股定理求出EA,得出BE=CE=6,由(2)的结论求出EH,然后根据勾股定理求出BH即可.
试题解析:(1)∵∠ODB=∠AEC,∠AEC=∠ABC,∴∠ODB=∠ABC,
∵OF⊥BC,∴∠BFD=90°,∴∠ODB+∠DBF=90°,∴∠ABC+∠DBF=90°,
即∠OBD=90°,∴BD⊥OB,∴BD是⊙O的切线;
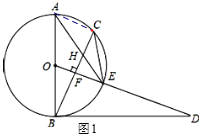
(2)连接AC,如图1所示:
∵OF⊥BC,∴![]() , ∴∠CAE=∠ECB,
, ∴∠CAE=∠ECB,
∵∠CEA=∠HEC,∴△CEH∽△AEC,∴![]() ,∴CE2=EHEA;
,∴CE2=EHEA;
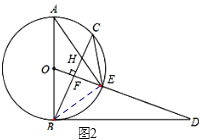
(3)连接BE,如图2所示:
∵AB是⊙O的直径,∴∠AEB=90°,
∵⊙O的半径为![]() ,sin∠BAE=
,sin∠BAE=![]() ,∴AB=5,BE=ABsin∠BAE=5×
,∴AB=5,BE=ABsin∠BAE=5×![]() =3,∴EA=
=3,∴EA=![]() =4,
=4,
∵![]() ,∴BE=CE=3,∵CE2=EHEA,∴EH=
,∴BE=CE=3,∵CE2=EHEA,∴EH=![]()
∴在Rt△ BEH中,BH=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级(2)班40个学生某次数学测验成绩如下:
63,84,91,53,69,81,61,69,91,78,75,81,80,67,76,81,79,94,61,69,
89,70,70,87,81,86,90,88,85,67,71,82,87,75,87,95,53,65,74,77
数学老师按10分的组距分段,算出每个分数段学生成绩出现的频数,填入频数分页表:
(1)请把频数分布表、频数分布直方图补充完整并画出频数分布折线图;
(2)请你帮老师统计一下这次数学考试的及格率(60分以上含60分为及格)及优秀率(90分以上含90分为优秀);
(3)请说明哪个分数段的学生最多?哪个分数段的学生最少?


-
科目: 来源: 题型:
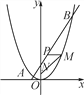
查看答案和解析>>【题目】如图,已知一条直线过点(0,4),且与抛物线y=
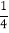 x2交于A,B两点,其中点A的横坐标是-2.
x2交于A,B两点,其中点A的横坐标是-2.(1)求这条直线的解析式及点B的坐标;
(2)在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)过线段AB上一点P,作PM∥x轴,交抛物线于点M,点M在第一象限,点N(0,1),当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若向东走20米记为+20米,则﹣50米表示( )
A.向东走50米
B.向西走50米
C.向南走50米
D.向北走50米 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若将半径为6cm的圆形纸片剪去三分之一,剩下的部分围成一个圆锥的侧面,则围成圆锥的全面积为__________.
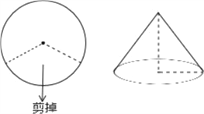
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长是2,点E是射线AB上一动点(点E与点A、B不重合),过点E作FG⊥DE交射线CB于点F、交DA的延长线于点G.
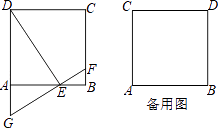
(1)求证:DE=GF.
(2)连结DF,设AE=x,△DFG的面积为y,求y与x之间的函数解析式.
(3)当Rt△AEG有一个角为30°时,求线段AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )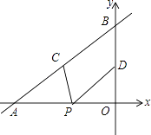
A.(﹣3,0)
B.(﹣6,0)
C.(﹣ ,0)
,0)
D.(﹣ ,0)
,0)
相关试题

