【题目】如图,正方形ABCD的边长是2,点E是射线AB上一动点(点E与点A、B不重合),过点E作FG⊥DE交射线CB于点F、交DA的延长线于点G.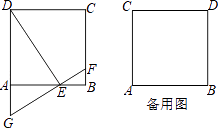
(1)求证:DE=GF.
(2)连结DF,设AE=x,△DFG的面积为y,求y与x之间的函数解析式.
(3)当Rt△AEG有一个角为30°时,求线段AE的长.
参考答案:
【答案】
(1)证明:过点F作FH⊥DA,垂足为H,
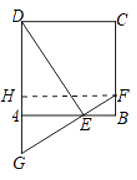
∵在正方形ABCD中,∠DAE=∠B=90°,
∴四边形ABFH是矩形,
∴FH=AB=DA,
∵DE⊥FG,
∴∠G=90°﹣∠ADE=∠DEA,
又∴∠DAE=∠FHG=90°,
∴△FHG≌△DAE,
∴DE=GF
(2)解:∵△FHG≌△DAE
∴FG=DE= ![]() ,
,
∵S△DGF= ![]() FGDE,
FGDE,
∴y= ![]() ,
,
∴解析式为:y= ![]() (0<x<2)
(0<x<2)
(3)解:①当∠AEG=30°时,
在Rt△ADE中,∵∠DAE=90°,AD=2,∠AED=90°﹣30°=60°,
∴AE=ADtan30°= ![]() ,
,
②当∠AEG=60°时,
在Rt△ADE中,∵∠DAE=90°,AD=2,∠AED=90°﹣60°=30°,
∴AE=ADtan60°=2 ![]() ,
,
综上所述,满足条件的AE的值为2 ![]() 或
或 ![]() .
.
【解析】(1)过点F作FH⊥DA,垂足为H,只要证明,△FHG≌△DAE即可解决问题;(2)由(1)可知DE=FG,所以△DGF的底与高可以关键勾股定理用含x的式子表示出来,所以解析式就可以表示出来;(3)分两种切线画出图形分别解决即可;
【考点精析】掌握正方形的性质是解答本题的根本,需要知道正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若向东走20米记为+20米,则﹣50米表示( )
A.向东走50米
B.向西走50米
C.向南走50米
D.向北走50米 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EHEA;
(3)若⊙O的直径为5,sinA=
 ,求BH的长.
,求BH的长.
-
科目: 来源: 题型:
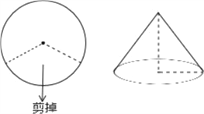
查看答案和解析>>【题目】如图,若将半径为6cm的圆形纸片剪去三分之一,剩下的部分围成一个圆锥的侧面,则围成圆锥的全面积为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )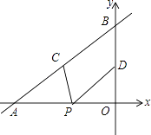
A.(﹣3,0)
B.(﹣6,0)
C.(﹣ ,0)
,0)
D.(﹣ ,0)
,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】国家体育馆“鸟巢”的建筑面积达25.8万平方米,请将“25.8万”用科学记数法表示,结果是( )
A.25.8×104B.25.8×105C.2.58×104D.2.58×105
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

相关试题

