Question

【题目】已知：在△ABC中，
（1）AC=BC，∠ACB=90°，CD⊥AB，点E是AB边上一点，点F在线段CE上，且△CBF≌△EBF（如图①），求证：CE平分∠ACD；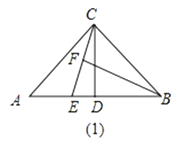
（2）除去（1）中条件“AC=BC”，其余条件不变（如图②），上述结论是否成立？并说明理由．

Answer 1

【答案】
（1）证明：∵AC=BC，∠ACB=90°，∠A=∠ABC=45°，

∵CD⊥AB，

∴∠CDB=90°，

∴∠BCD=45°，

∴∠BCD=∠A，

∵△CBF≌△EBF，

∴∠BCF=∠BEF

∵∠BEF是△ACE的外角，

∴∠BEF=∠A+∠ACE，

又∵∠BCF=∠BCD+∠DCE

∴∠A+∠ACE=∠BCD+∠DCE

∴∠ACE=∠DCE

∴CE平分∠ACD

（2）上述结论依然成立，

∵∠ACB=90°，CD⊥AB，

∴∠A+∠ABC=90°，∠BCD+∠ABC=90°，

∴∠BCD=∠A．

∵△CBF≌△EBF，

∴∠BCF=∠BEF

∵∠BEF是△ACE的外角，

∴∠BEF=∠A+∠ACE，

又∵∠BCF=∠BCD+∠DCE

∴∠A+∠ACE=∠BCD+∠DCE

∴∠ACE=∠DCE

∴CE平分∠ACD

【解析】（1）先证明△CBF≌△EBF，再根据外角的性质，得∠BEF=∠A+∠ACE，即可得出∠ACE=∠DCE，则CE平分∠ACD；（2）假设结论依然成立，由△CBF≌△EBF，得∠BCF=∠BEF，再由外角，得∠BEF=∠A+∠ACE，即可得出CE平分∠ACD．
【考点精析】本题主要考查了角平分线的性质定理的相关知识点，需要掌握定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上才能正确解答此题．