【题目】如图,已知坐标系中点A(2,-1),B(7,-1),C(3,-3).
(1)判定△ABC的形状;
(2)设△ABC关于x轴的对称图形是△A1B1C1,若把△A1B1C1的各顶点的横坐标都加2.纵坐标不变,则△A1B1C1的位置发生什么变化?若最终位置是△A2B2C2,求C2点的坐标;
(3)试问在x轴上是否存在一点P,使PC-PB最大,若存在,求出PC-PB的最大值及P点坐标;若不存在,说明理由.

参考答案:
【答案】(1)△ABC是直角三角形;(2)图像向右平移2个单位,C2坐标为(5,2);(3)y=![]() x-
x-![]() ;P(9,0).
;P(9,0).
【解析】分析:(1)计算出A![]() ,B
,B![]() ,A
,A![]() ,比较数量关系即可;
,比较数量关系即可;
(2)把△![]() 的各顶点的横坐标都加2.纵坐标不变,则图形向右移动两个单位;
的各顶点的横坐标都加2.纵坐标不变,则图形向右移动两个单位;
(3)连接C![]() ,与x轴的交点即为P,设BC对应一次函数为y=kx+b,联立方程组即可求出点P坐标.
,与x轴的交点即为P,设BC对应一次函数为y=kx+b,联立方程组即可求出点P坐标.
本题解析:
解:(1)∵AC2=22+12=5,BC2=42+22=20,AB2=52
∴AC2+BC2=AB2
∴△ABC是直角三角形

(2)图像向右平移2个单位,C2坐标为(5,2)
(3)存在.连接CB1,与x轴的交点即为P.
理由:设BC对应一次函数为y=kx+b
∵C(3,-3) B(7,-1)
∴![]()
∴
∴y=![]() x-
x-![]()
令y=0得x=9
∴P(9,0)
-
科目: 来源: 题型:
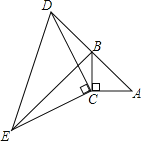
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰直角三角形CDE,其中∠DCE=90°,连接BE.
(1)求证:△ACD≌△BCE;
(2)若AC=3,求BE的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,已知点C在线段AB上,且AC=6cm,BC=4cm,点M,N分别是AC,BC的中点,求线段MN的长度.

(2)在(1)中,如果AC=acm,BC=bcm,其它条件不变,你能猜出MN的长度吗?请你用一句简洁的话表述你发现的规律.
(3)对于(1)题,如果我们这样叙述它:“已知线段AC=6cm,BC=4cm,点C在直线AB上,点M,N分别是AC,BC的中点,求MN的长度.”结果会有变化吗?如果有,求出结果.
-
科目: 来源: 题型:
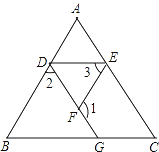
查看答案和解析>>【题目】如图,已知∠1+∠2=180°,∠B=∠3,你能判断∠C与∠AED的大小关系吗?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小丽做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数n
100
200
300
500
800
1000
3000
摸到白球的次数m
63
124
178
302
481
599
1803
摸到白球的频率

0.63
0.62
0.593
0.604
0.601
0.599
0.601
(1)请估计:当实验次数为10000次时,摸到白球的频率将会接近 ;(精确到0.1)
(2)假如由你摸球一次,你摸到白球的概率P(摸到白球)= ;
(3)盒子中有黑球 个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中,①∠A+∠B=∠C; ②∠A:∠B:∠C=1:2:3; ③∠A=
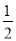 ∠B=
∠B=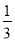 ∠C;
∠C;④∠A=∠B=2∠C; ⑤∠A=2∠B=3∠C,能确定△ABC为直角三角形的条件有( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一条长为60cm的卷尺铺平后折叠,使得卷尺自身的一部分重合,然后在重合部分(阴影处)沿与卷尺边垂直的方向剪一刀,此时卷尺分为了三段,若这三段长度由短到长的比为1:2:3,则折痕对应的刻度的可能性有 ( )
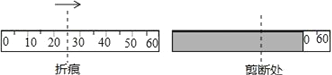
A. 4种 B. 5种 C. 6种 D. 7种
相关试题

