【题目】如图,四边形ABCD为正方形,点A坐标为(0,1),点B坐标为(0,﹣2),反比例函数y= ![]() 的图象经过点C,一次函数y=ax+b的图象经过A,C两点.
的图象经过点C,一次函数y=ax+b的图象经过A,C两点. 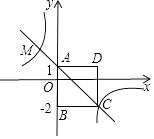
(1)求反比例函数与一次函数的解析式;
(2)若点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标.
参考答案:
【答案】
(1)解:∵点A的坐标为(0,1),点B的坐标为(0,﹣2),
∴AB=1+2=3,
∵四边形ABCD为正方形,
∴Bc=3,
∴C(3,﹣2),
把C(3,﹣2)代入y= ![]() 得k=3×(﹣2)=﹣6,
得k=3×(﹣2)=﹣6,
∴反比例函数解析式为y=﹣ ![]() ,
,
把C(3,﹣2),A(0,1)代入y=ax+b得 ![]() ,
,
解得 ![]() ,
,
∴一次函数解析式为y=﹣x+1
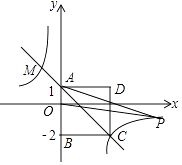
(2)解:设P(t,﹣ ![]() ),
),
∵△OAP的面积恰好等于正方形ABCD的面积,
∴ ![]() ×1×|t|=3×3,解得t=18或t=﹣18,
×1×|t|=3×3,解得t=18或t=﹣18,
∴P点坐标为(18,﹣ ![]() )或(﹣18,
)或(﹣18, ![]() ).
).
【解析】(1)先根据A点和B点坐标得到正方形的边长,则BC=3,于是可得到C(3,﹣2),然后利用待定系数法求反比例函数与一次函数的解析式;(2)设P(t,﹣ ![]() ),根据三角形面积公式和正方形面积公式得到
),根据三角形面积公式和正方形面积公式得到 ![]() ×1×|t|=3×3,然后解绝对值方程求出t即可得到P点坐标.
×1×|t|=3×3,然后解绝对值方程求出t即可得到P点坐标.
【考点精析】利用正方形的性质对题目进行判断即可得到答案,需要熟知正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AC=BC,∠ACB=120°,点D在AB边上运动(D不与A、B重合),连结CD.作∠CDE=30°,DE交AC于点E.

(1)当DE∥BC时,△ACD的形状按角分类是直角三角形;
(2)在点D的运动过程中,△ECD的形状可以是等腰三角形吗?若可以,请求出∠AED的度数;若不可以,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E,H分别在AB、AC上,已知BC=40cm,AD=30cm.
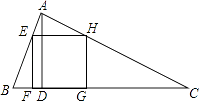
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠C=90°,D是AB的中点,DE⊥DF,点E,F分别在AC,BC上,求证:DE=DF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
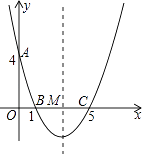
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
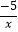 ,下列结论中不正确的是( )
,下列结论中不正确的是( )
A.图象必经过点(1,﹣5)
B.y随x的增大而增大
C.图象在第二、四象限内
D.若x>1,则﹣5<y<0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )

A.点(0,3)
B.点(2,3)
C.点(5,1)
D.点(6,1)
相关试题

