【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E,H分别在AB、AC上,已知BC=40cm,AD=30cm. 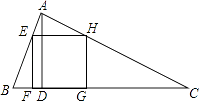
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与周长.
参考答案:
【答案】
(1)解:∵四边形EFGH是正方形,
∴EH∥BC,
∴∠AEH=∠B,∠AHE=∠C,
∴△AEH∽△ABC
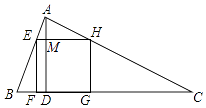
(2)解:如图,设AD与EH交于点M,
∵∠EFD=∠FEM=∠FDM=90°,
∴四边形EFDM是矩形,
∴EF=DM,
设正方形EFGH的边长为x,则DM=x,AM=30﹣x,
∵△AEH∽△ABC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得x= ![]() ,
,
∴正方形EFGH的边长为 ![]() cm,周长为
cm,周长为 ![]() cm.
cm.
【解析】(1)根据四边形EFGH是正方形,得到EH∥BC,进而得出∠AEH=∠B,∠AHE=∠C,即可判定△AEH∽△ABC;(2)设正方形EFGH的边长为x,则DM=x,AM=30﹣x,根据△AEH∽△ABC,得出 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,进而解得x=
,进而解得x= ![]() ,即可得出正方形的边长与周长.
,即可得出正方形的边长与周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P.
(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.

-
科目: 来源: 题型:
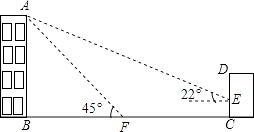
查看答案和解析>>【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上).
(参考数据:sin22°≈ ,cos22°
,cos22° 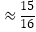 ,tan22
,tan22  )
)
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AC=BC,∠ACB=120°,点D在AB边上运动(D不与A、B重合),连结CD.作∠CDE=30°,DE交AC于点E.

(1)当DE∥BC时,△ACD的形状按角分类是直角三角形;
(2)在点D的运动过程中,△ECD的形状可以是等腰三角形吗?若可以,请求出∠AED的度数;若不可以,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠C=90°,D是AB的中点,DE⊥DF,点E,F分别在AC,BC上,求证:DE=DF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为正方形,点A坐标为(0,1),点B坐标为(0,﹣2),反比例函数y=
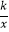 的图象经过点C,一次函数y=ax+b的图象经过A,C两点.
的图象经过点C,一次函数y=ax+b的图象经过A,C两点. 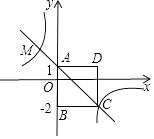
(1)求反比例函数与一次函数的解析式;
(2)若点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
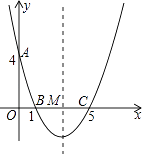
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
相关试题

