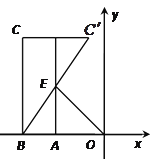
【题目】如图, 已知点A的坐标为(m,0)点B的坐标为(![]() ,0),在x轴上方取点C,使CB⊥x轴,且CB=2AO,点C,
,0),在x轴上方取点C,使CB⊥x轴,且CB=2AO,点C, ![]() 关于直线
关于直线![]() 对称,
对称, ![]() 交直线
交直线![]() 于点E若△BOE的面积为4,则点E的坐标为_______.
于点E若△BOE的面积为4,则点E的坐标为_______.
参考答案:
【答案】(4,4)或![]()
【解析】先根据矩形的性质与轴对称的性质得出AB=C′D,再利用AAS证明△ABE≌△DC′E,得出AE=DE=﹣m.根据△BOE的面积为4,列出方程(2﹣m)(﹣m)=4,解方程即可.
如图,设AE与CC′交于点D.
∵点A的坐标为(m,0),在x轴上方取点C,使CB⊥x轴,且CB=2AO, ∴CB=﹣2m.
∵点C,C′关于直线x=m对称,
∴CD=C′D,
∵ABCD是矩形,AB=CD,
∴AB=C′D.
又∵∠BAE=∠C′DE=90°,∠AEB=DEC′,
∴△ABE≌△DC′E,
∴AE=DE,
∴AE=AD=BC=﹣m.
∵△BOE的面积为4,
∴(2﹣m)(﹣m)=4,
整理得,m2﹣2m﹣8=0,
解得m=4或﹣2,
∵在x轴上方取点C,
∴﹣2m>0,
∴m<0,
∴m=4不合题意舍去,
“点睛”本题考查了矩形的性质,轴对称的性质,全等三角形的与性质,三角形的面积,得出AE=DE=﹣m是解题关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,六边形ABCDEF的内角都相等,CF∥AB.
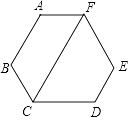
(1)求∠FCD的度数;
(2)求证:AF∥CD. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2+b2-8a-10b+41=0,求5a-b2+25的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:n(m﹣n)(p﹣q)﹣n(n﹣m)(p﹣q)=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】放学时,王老师布置了一道因式分解题:(x+y)2+4(x-y)2-4(x2-y2),小明思考了半天,没有得出答案.请你帮小明解决这个问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验探究:
(1)动手操作:
①如图1,将一块直角三角板DEF放置在直角三角板ABC上,使三角板DEF的两条直角边DE、DF分别经过点B、C,且BC∥EF,已知∠A=30°,则∠ABD+∠ACD=;
②如图2,若直角三角板ABC不动,改变等腰直角三角板DEF的位置,使三角板DEF的两条直角边DE、DF仍然分别经过点B、C,那么∠ABD+∠ACD=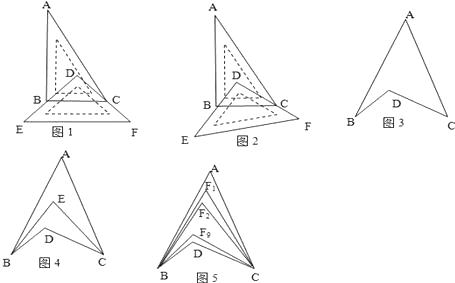
(2)猜想证明:
如图3,∠BDC与∠A、∠B、∠C之间存在着什么关系,并说明理由;
(3)灵活应用:
请你直接利用以上结论,解决以下列问题:
①如图4,BE平分∠ABD,CE平分∠ACB,若∠BAC=40°,∠BDC=120°,求∠BEC的度数;
(4)②如图5,∠ABD,∠ACD的10等分线相交于点F1、F2、…、F9 ,
若∠BDC=120°,∠BF3C=64°,则∠A的度数为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,作AD⊥AB交BC的延长线于点D,作CE⊥AC,且使AE∥BD,连结DE.
(1)求证:AD=CE.
(2)若DE=3,CE=4,求tan∠DAE的值.

相关试题

