【题目】已知A,B两地相距120千米,甲乙两人沿同一条公路匀速行驶,甲骑自行车以20千米/时从A地前往B地,同时乙骑摩托车从B地前往A地,设两人之间的距离为s(千米),甲行驶的时间为t(小时),若s与t的函数关系如图所示,则下列说法错误的是( )

A.经过2小时两人相遇
B.若乙行驶的路程是甲的2倍,则t=3
C.当乙到达终点时,甲离终点还有60千米
D.若两人相距90千米,则t=0.5或t=4.5
参考答案:
【答案】B
【解析】
由图象得到经过2小时两人相遇,A选项正确,由于乙的速度是![]() =40千米/时,乙的速度是甲的速度的2倍可知B选项错误,计算出乙到达终点时,甲走的路程,可得C选项正确,当0<t≤2时,得到t=0.5,当3<t≤6时,得到t=4.5,于是得到若两人相距90千米,则t=0.5或t=4.5,故D正确.
=40千米/时,乙的速度是甲的速度的2倍可知B选项错误,计算出乙到达终点时,甲走的路程,可得C选项正确,当0<t≤2时,得到t=0.5,当3<t≤6时,得到t=4.5,于是得到若两人相距90千米,则t=0.5或t=4.5,故D正确.
由图象知:经过2小时两人相遇,A选项正确;
甲的速度是20千米/小时,则乙的速度是![]() =40千米/时,乙的速度是甲的速度的2倍,所以在乙到达终点之前,乙行驶的路程都是甲的二倍,B选项错误;
=40千米/时,乙的速度是甲的速度的2倍,所以在乙到达终点之前,乙行驶的路程都是甲的二倍,B选项错误;
乙到达终点时所需时间为![]() =3(小时),3小时甲行驶3×20=60(千米),离终点还有120-60=60(千米),故C选项正确,
=3(小时),3小时甲行驶3×20=60(千米),离终点还有120-60=60(千米),故C选项正确,
当0<t≤2时,S=-60t+120,当S=90时,即-60t+120=90,解得:t=0.5,
当3<t≤6时,S=20t,当S=90时,即20t=90,解得:t=4.5,
∴若两人相距90千米,则t=0.5或t=4.5,故D正确.
故选B.
-
科目: 来源: 题型:
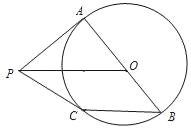
查看答案和解析>>【题目】如图,AB是⊙O的直径,PA是⊙O的切线,点C在⊙O上,CB∥PO.
(1)判断PC与⊙O的位置关系,并说明理由;
(2)若AB=6,CB=4,求PC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在1000个“○”中依次填入一列数字
 使得其中任意四个相邻“○”中所填数字之和都等于
使得其中任意四个相邻“○”中所填数字之和都等于 ,已知
,已知 ,
, ,则
,则 的值为( )
的值为( )
A.1B.
 C.2D.
C.2D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6.点P从点A出发,沿AC以每秒1个单位的速度向终点C运动;点Q从点C出发,沿C-B-A以每秒2个单位的速度向终点A运动.当点P停止运动时,点Q也随之停止.点P、Q同时出发,设点P的运动时间为t(秒).
(1)求AB的长.
(2)用含t的代数式表示CP的长.
(3)设点Q到CA的距离为y,求y与t之间的函数关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),公路上有A、B、C三个车站,一辆汽车从A站以速度v1匀速驶向B站,到达B站后不停留,以速度v2匀速驶向C站,汽车行驶路程y(千米)与行驶时间x(小时)之间的函数图象如图(2)所示.
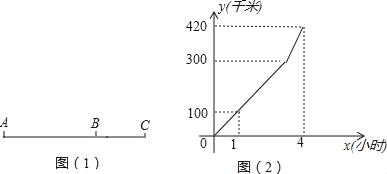
(1)当汽车在A、B两站之间匀速行驶时,求y与x之间的函数关系式及自变量的取值范围;
(2)求出v2的值;
(3)若汽车在某一段路程内刚好用50分钟行驶了90千米,求这段路程开始时x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学中,为了书写简便,18世纪数学家欧拉就引进了求和符号“∑”.记,
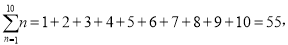
 ,
,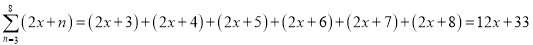 .
.同学们,通过以上材料的阅读,请回答下列问题:
(1)计算(填写最后的结果)
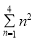 =__________;
=__________; ____________.
____________.(2)2+4+6+8+10用求和公式符号可表示为__________.
(3)化简:
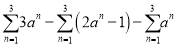
(4)若对于任意x都存在
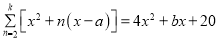 ,请求代数式
,请求代数式 b-ab的值.
b-ab的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△A1C1C2的周长为1,作C1D1⊥A1C2于D1,在C1C2的延长线上取点C3,使D1C3=D1C1,连接D1C3,以C2C3为边作等边△A2C2C3;作C2D2⊥A2C3于D2,在C2C3的延长线上取点C4,使D2C4=D2C2,连接D2C4,以C3C4为边作等边△A3C3C4;…且点A1,A2,A3,…都在直线C1C2同侧,如此下去,则△A1C1C2,△A2C2C3,△A3C3C4,…,△AnCnCn+1的周长和为______.(n≥2,且n为整数)

相关试题

