【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6.点P从点A出发,沿AC以每秒1个单位的速度向终点C运动;点Q从点C出发,沿C-B-A以每秒2个单位的速度向终点A运动.当点P停止运动时,点Q也随之停止.点P、Q同时出发,设点P的运动时间为t(秒).
(1)求AB的长.
(2)用含t的代数式表示CP的长.
(3)设点Q到CA的距离为y,求y与t之间的函数关系式.

参考答案:
【答案】(1)10;(2)8-t; (3)y=2t(0≤t≤3);y=![]() (3<t≤8)
(3<t≤8)
【解析】
(1)在△ABC中,由勾股定理,求出AB的长是多少即可.
(2)首先求出AP的长度,然后用AC的长度减去AP的长度,求出CP的长度是多少即可.
(3)根据题意,分两种情况:①当0≤t≤3时;②当3<t≤8时;求出y与t之间的函数关系式即可.
(1)如图1,
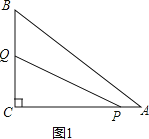
∵∠ACB=90°,AC=8,BC=6,
∴AB=![]() =10.
=10.
(2)∵点P从点A出发,沿AC以每秒1个单位的速度向终点C运动,
∴AP=t,
又∵AC=8,
∴CP=8-t.
(3)①如图2,当0≤t≤3时,
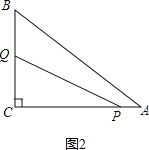 ,
,
∵点Q从点C出发,沿C-B-A以每秒2个单位的速度向终点A运动,
∴y=QC=2t.
②如图3,当3<t≤8时,如图,作QD⊥AC于点D,
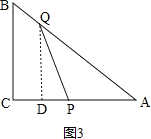 ,
,
∵sinA=![]() ,
,
∴![]() ,
,
∴y=-![]() t+
t+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某淘宝网店销售台灯,每个台灯售价为60元,每星期可卖出300个,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30个.已知该款台灯每个成本为40元,
(1)若每个台灯降x元(
 ),则每星期能卖出 个台灯,每个台灯的利润是 元.
),则每星期能卖出 个台灯,每个台灯的利润是 元. (2)在顾客得实惠的前提下,该淘宝网店还想获得6480元的利润,应将每件的售价定为多少元?
-
科目: 来源: 题型:
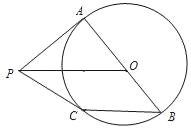
查看答案和解析>>【题目】如图,AB是⊙O的直径,PA是⊙O的切线,点C在⊙O上,CB∥PO.
(1)判断PC与⊙O的位置关系,并说明理由;
(2)若AB=6,CB=4,求PC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在1000个“○”中依次填入一列数字
 使得其中任意四个相邻“○”中所填数字之和都等于
使得其中任意四个相邻“○”中所填数字之和都等于 ,已知
,已知 ,
, ,则
,则 的值为( )
的值为( )
A.1B.
 C.2D.
C.2D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A,B两地相距120千米,甲乙两人沿同一条公路匀速行驶,甲骑自行车以20千米/时从A地前往B地,同时乙骑摩托车从B地前往A地,设两人之间的距离为s(千米),甲行驶的时间为t(小时),若s与t的函数关系如图所示,则下列说法错误的是( )

A.经过2小时两人相遇
B.若乙行驶的路程是甲的2倍,则t=3
C.当乙到达终点时,甲离终点还有60千米
D.若两人相距90千米,则t=0.5或t=4.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),公路上有A、B、C三个车站,一辆汽车从A站以速度v1匀速驶向B站,到达B站后不停留,以速度v2匀速驶向C站,汽车行驶路程y(千米)与行驶时间x(小时)之间的函数图象如图(2)所示.
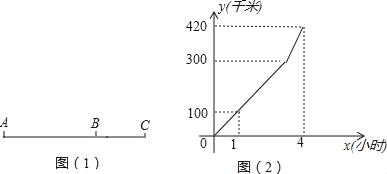
(1)当汽车在A、B两站之间匀速行驶时,求y与x之间的函数关系式及自变量的取值范围;
(2)求出v2的值;
(3)若汽车在某一段路程内刚好用50分钟行驶了90千米,求这段路程开始时x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学中,为了书写简便,18世纪数学家欧拉就引进了求和符号“∑”.记,
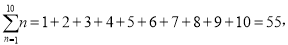
 ,
,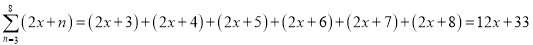 .
.同学们,通过以上材料的阅读,请回答下列问题:
(1)计算(填写最后的结果)
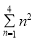 =__________;
=__________; ____________.
____________.(2)2+4+6+8+10用求和公式符号可表示为__________.
(3)化简:
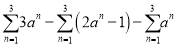
(4)若对于任意x都存在
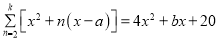 ,请求代数式
,请求代数式 b-ab的值.
b-ab的值.
相关试题

