【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
(1)已知BD=![]() ,求正方形ABCD的边长;
,求正方形ABCD的边长;
(2)猜想线段EM与CN的数量关系并加以证明.

参考答案:
【答案】(1)1;(2)CN=![]() CM.
CM.
【解析】
试题分析:(1)根据正方形的性质以及勾股定理即可求得;
(2)根据等腰三角形三线合一的性质证得CE⊥AF,进一步得出∠BAF=∠BCN,然后通过证得△ABF≌△CBN得出AF=CN,进而证得△ABF∽△COM,根据相似三角形的性质和正方形的性质即可证得CN=![]() CM.
CM.
试题解析:(1)∵四边形ABCD是正方形,∴△ABD是等腰直角三角形,∴2AB2=BD2,∵BD=![]() ,∴AB=1,∴正方形ABCD的边长为1;
,∴AB=1,∴正方形ABCD的边长为1;
(2)CN=![]() CM.
CM.
证明:∵CF=CA,AF是∠ACF的平分线,∴CE⊥AF,∴∠AEN=∠CBN=90°,∵∠ANE=∠CNB,∴∠BAF=∠BCN,在△ABF和△CBN中,∵∠BAF=∠BCN,∠ABF=∠CBN,AB=BC,∴△ABF≌△CBN(AAS),∴AF=CN,∵∠BAF=∠BCN,∠ACN=∠BCN,∴∠BAF=∠OCM,∵四边形ABCD是正方形,∴AC⊥BD,∴∠ABF=∠COM=90°,∴△ABF∽△COM,∴![]() ,∴
,∴![]() ,即CN=
,即CN=![]() CM.
CM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B.C在同一水平地面上.
(1)求斜坡AB的水平宽度BC;
(2)矩形DEFG为长方体货柜的侧面图,其中DE=2.5m,EF=2m,将该货柜沿斜坡向上运送,当BF=3.5m时,求点D离地面的高.(
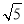 ≈2.236,结果精确到0.1m)
≈2.236,结果精确到0.1m)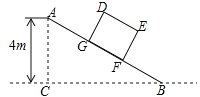
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.求证:
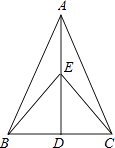
(1)△ABD≌△ACD;
(2)BE=CE. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,我们在2016年1月的日历中标出一个十字星,并计算它的“十字差”(将十字星左右两数,上下两数分别相乘再将所得的积作差,称为该十字星的“十字差”).该十字星的十字差为12×14﹣6×20=48,再选择其它位置的十字星,可以发现“十字差”仍为48.
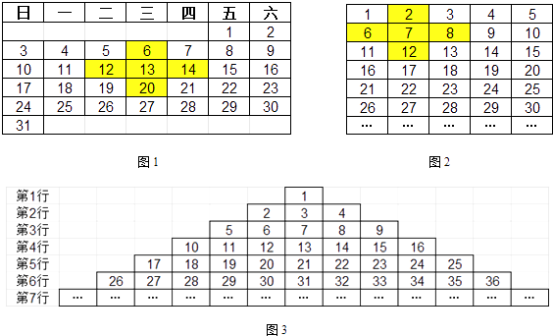
(1)如图2,将正整数依次填入5列的长方形数表中,探究不同位置十字星的“十字差”,可以发现相应的“十字差”也是一个定值,则这个定值为 .
(2)若将正整数依次填入k列的长方形数表中(k≥3),继续前面的探究,可以发现相应“十字差”为与列数k有关的定值,请用k表示出这个定值,并证明你的结论.
(3)如图3,将正整数依次填入三角形的数表中,探究不同十字星的“十字差”,若某个十字星中心的数在第32行,且其相应的“十字差”为2015,则这个十字星中心的数为(直接写出结果). -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,AC⊥BD,顺次连接它的各边中点所得的四边形是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在有理数中,绝对值等于它本身的数有( )
A.1个
B.2个
C.3个
D.无穷多个 -
科目: 来源: 题型:
查看答案和解析>>【题目】综合题:解下列各式
(1)解方程组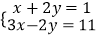
(2)解不等式组: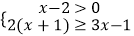 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
相关试题

