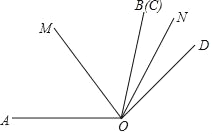
【题目】如图,∠AOB=α,∠COD=β(α>β),OC与OB重合,OD在∠AOB外,射线OM、ON分别是∠AOC、∠BOD的角平分线.
(1)①若α=100°,β=60°,则∠MON等于多少;
②在①的条件下∠COD绕点O逆时针旋转n°(0<n<100(且n≠60)时,求∠MON的度数;
(2)直接写出∠COD绕点O逆时针旋转n°(0<n<360)时∠MON的值(用含α、β的式子表示).
参考答案:
【答案】(1)①∠MON=80°;②∠MON=80°;(2)∠MON=![]() (α+β)或180°﹣
(α+β)或180°﹣![]() (α+β).
(α+β).
【解析】
(1)①根据角平分线的定义求出∠BOM和∠CON的度数,然后相加即可得出答案;
②根据旋转的性质可知∠BOC=n°,分两种情况进行讨论:如图1,∠BOD=60°﹣n°,∠AOC=100°﹣n°,根据角平分线的定义得出∠COM和∠BON的度数,然后根据∠MON=∠COM+∠COB+∠BON进行计算即可得出结论;如图2,∠BOD=n°﹣60°,∠AOC=100°﹣n°,根据角平分线的定义得出∠COM和∠BON的度数,然后根据∠MON=∠COM+∠COD+∠BON进行计算即可得出结论;
(2)根据①、②的解题思路即可得到结论.
(1)①∵OM,ON分别是∠AOC,∠BOD的角平分线,
∴∠BOM=![]() ∠AOB,∠BON=
∠AOB,∠BON=![]() ∠BOD,
∠BOD,
∴∠MON=![]() (∠AOB+∠BOD),
(∠AOB+∠BOD),
又∵∠AOB=100°,∠COD=60°,
∴∠MON=![]() (∠AOB+∠BOD)=
(∠AOB+∠BOD)=![]() ×(100°+60°)=80°.
×(100°+60°)=80°.
②如图1,∵∠COD绕点O逆时针旋转n°,
∴∠BOC=n°,
∴∠BOD=60°﹣n°,∠AOC=100°﹣n°,
∵OM,ON分别是∠AOC,∠BOD的角平分线,
∴∠COM=![]() ∠AOC=50°﹣
∠AOC=50°﹣![]() n°,∠BON=
n°,∠BON=![]() ∠BOD=30°﹣
∠BOD=30°﹣![]() n°,
n°,
∴∠MON=∠COM+∠COB+∠BON=80°;
如图2,∵∠COD绕点O逆时针旋转n°,
∴∠BOC=n°,
∴∠BOD=n°﹣60°,∠AOC=100°﹣n°,
∵OM,ON分别是∠AOC,∠BOD的角平分线,
∴∠COM=![]() ∠AOC=50°﹣
∠AOC=50°﹣![]() n°,∠DON=
n°,∠DON=![]() ∠BOD=
∠BOD=![]() n°﹣30°,
n°﹣30°,
∴∠MON=∠COM+∠COD+∠DON=80°;
(2)∵OM为∠AOD的平分线,ON为∠BOC的平分线,∠AOB=α,∠COD=β,
∴∠MON=![]() (α+β)或180°﹣
(α+β)或180°﹣![]() (α+β);
(α+β);

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在R t△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.

(1)动手操作:利用尺规作,以AB边上一点O为圆心,过A,D两点作⊙O,与AB的另一个交点为E,与AC的另一个交点为F(不写作法,保留作图痕迹),再判断直线BC与⊙O的位置关系,并说明理由。
(2)若∠BAC=60度,CD= ,求线段BD、BE与劣弧DE所围成的图形面积.(结果保留根号和
,求线段BD、BE与劣弧DE所围成的图形面积.(结果保留根号和  )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】王华在学习相似三角形时,在北京市义务教育课程改革实验教材第17册书,第31页遇到这样一道题:
如图1,在△ABC中,P是边AB上的一点,联结CP.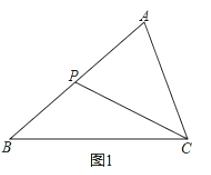
要使△ACP∽△ABC,还需要补充的一个条件是__,或__.
(1)王华补充的条件是 , 或 .
(2)请你参考上面的图形和结论,探究、解答下面的问题:
如图2,在△ABC中,∠A=30°,AC2= AB2+AB.BC.
求∠C的度数.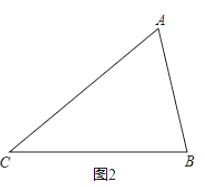
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:P、Q分别是两条线段a和b上任意一点,线段PQ的长度的最小值叫做线段a与线段b的距离.
已知O(0,0),A(4,0),B(m,n),C(m+4,n)是平面直角坐标系中四点.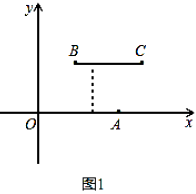
(1)根据上述定义,当m=2,n=2时,如图1,线段BC与线段OA的距离是;当m=5,n=2时,如图2,线段BC与线段OA的距离为;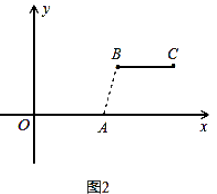
(2)如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式.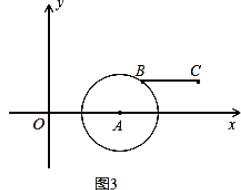
(3)当m的值变化时,动线段BC与线段OA的距离始终为2,线段BC的中点为M,
①求出点M随线段BC运动所围成的封闭图形的周长;
②点D的坐标为(0,2),m≥0,n≥0,作MH⊥x轴,垂足为H,是否存在m的值使以A、M、H为顶点的三角形与△AOD相似?若存在,求出m的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式
B.平方差公式
C.两数和的完全平方公式
D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,A、B两点在数轴上对应的数分别为﹣12和4.
(1)直接写出A、B两点之间的距离;
(2)若在数轴上存在一点P,使得AP=
 PB,求点P表示的数.
PB,求点P表示的数.
(3)如图2,现有动点P、Q,若点P从点A出发,以每秒5个单位长度的速度沿数轴向右运动,同时点Q从点B出发,以每秒2个单位长度的速度沿数轴向左运动,当点Q到达原点O后立即以每秒3个单位长度的速度沿数轴向右运动,求:当OP=4OQ时的运动时间t的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解决问题:
一辆货车从超市出发,向东走了3千米到达小彬家,继续走2.5千米到达小颖家,然后向西走了10千米到达小明家,最后回到超市.
(1)以超市为原点,以向东的方向为正方向,用1个单位长度表示1千米,在数轴上表示出小明家,小彬家,小颖家的位置.
(2)小明家距小彬家多远?
(3)货车每千米耗油0.2升,这次共耗油多少升?
相关试题

