【题目】王华在学习相似三角形时,在北京市义务教育课程改革实验教材第17册书,第31页遇到这样一道题:
如图1,在△ABC中,P是边AB上的一点,联结CP.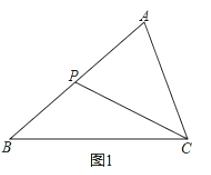
要使△ACP∽△ABC,还需要补充的一个条件是__,或__.
(1)王华补充的条件是 , 或 .
(2)请你参考上面的图形和结论,探究、解答下面的问题:
如图2,在△ABC中,∠A=30°,AC2= AB2+AB.BC.
求∠C的度数.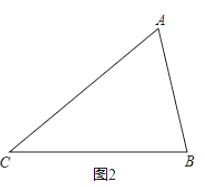
参考答案:
【答案】
(1)∠ACP=∠B(或∠APC=∠ACB),或AC2=AP?AB
(2)解:延长AB到点D,使BD=BC,连接CD,如图所示:
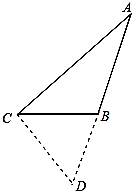
∵AC2=AB2+ABBC=AB(AB+BC)=AB(AB+BD)=ABAD,
∴ ![]() ,
,
又∵∠A=∠A,∴△ACB∽△ADC,
∴∠ACB=∠D,
∵BC=BD,
∴∠BCD=∠D,
在△ACD中,∠ACB+∠BCD+∠D+∠A=180°,
∴3∠ACB+30°=180°,
∴∠ACB=50°
【解析】解:(1)王华补充的条件是:∠ACP=∠B(或∠APC=∠ACB);或AC2=APAB;理由如下:
∵∠A=∠A,
∴当∠ACP=∠B,或∠APC=∠ACB;
或 ![]() ,即AC2=APAB时,△ACP∽△ABC;
,即AC2=APAB时,△ACP∽△ABC;
【考点精析】利用三角形的内角和外角和相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国明代珠算家程大位的名著《直指算法统宗》里有一道著名算题:“一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,试问大、小和尚各多少人?设大和尚有x人,依题意列方程得( )
A.
 +3(100﹣x)=100 B.
+3(100﹣x)=100 B.  ﹣3(100﹣x)=100
﹣3(100﹣x)=100C. 3x﹣
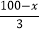 =100 D. 3x+
=100 D. 3x+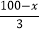 =100
=100 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于点D,DE⊥AB交AB的延长线于点E,DF⊥AC于点F,现有下列结论:①DE=DF;②DE+DF=AD;③DM平分∠ADF;④AB+AC=2AE.其中,正确的有( )
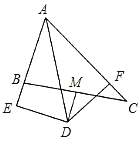
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在R t△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.

(1)动手操作:利用尺规作,以AB边上一点O为圆心,过A,D两点作⊙O,与AB的另一个交点为E,与AC的另一个交点为F(不写作法,保留作图痕迹),再判断直线BC与⊙O的位置关系,并说明理由。
(2)若∠BAC=60度,CD= ,求线段BD、BE与劣弧DE所围成的图形面积.(结果保留根号和
,求线段BD、BE与劣弧DE所围成的图形面积.(结果保留根号和  )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:P、Q分别是两条线段a和b上任意一点,线段PQ的长度的最小值叫做线段a与线段b的距离.
已知O(0,0),A(4,0),B(m,n),C(m+4,n)是平面直角坐标系中四点.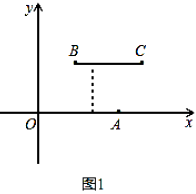
(1)根据上述定义,当m=2,n=2时,如图1,线段BC与线段OA的距离是;当m=5,n=2时,如图2,线段BC与线段OA的距离为;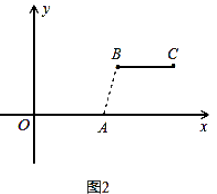
(2)如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式.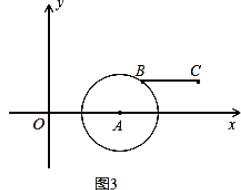
(3)当m的值变化时,动线段BC与线段OA的距离始终为2,线段BC的中点为M,
①求出点M随线段BC运动所围成的封闭图形的周长;
②点D的坐标为(0,2),m≥0,n≥0,作MH⊥x轴,垂足为H,是否存在m的值使以A、M、H为顶点的三角形与△AOD相似?若存在,求出m的值;若不存在,请说明理由. -
科目: 来源: 题型:
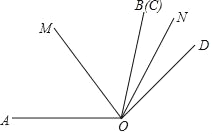
查看答案和解析>>【题目】如图,∠AOB=α,∠COD=β(α>β),OC与OB重合,OD在∠AOB外,射线OM、ON分别是∠AOC、∠BOD的角平分线.
(1)①若α=100°,β=60°,则∠MON等于多少;
②在①的条件下∠COD绕点O逆时针旋转n°(0<n<100(且n≠60)时,求∠MON的度数;
(2)直接写出∠COD绕点O逆时针旋转n°(0<n<360)时∠MON的值(用含α、β的式子表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式
B.平方差公式
C.两数和的完全平方公式
D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
相关试题

