【题目】新定义:对非负数“四舍五入”到个位的值记为![]() ,即当
,即当![]() 为非负整数时,若
为非负整数时,若![]() ,则
,则![]() 如:
如:![]() ,试解决下列问题
,试解决下列问题
(1)填空:①![]() ②若
②若![]() ,则实数
,则实数![]() 的取值范围为
的取值范围为
(2)在关于![]() 的方程组
的方程组![]() 中,若未知数
中,若未知数![]() 满足
满足![]() ,求
,求![]() 的值.
的值.
(3)当![]() 时,若
时,若![]() ,求
,求![]() 的最小值.
的最小值.
(4)求满足![]() 的所有非负实数
的所有非负实数![]() 的值,请直接写出答案 .
的值,请直接写出答案 .
参考答案:
【答案】(1)①3;②![]() ;(2)2;(3)0;(4)0或
;(2)2;(3)0;(4)0或![]()
【解析】
(1)①利用对非负实数x“四舍五入”到个位的值记为![]() ,进而得出
,进而得出![]() 的值;
的值;
②利用对非负实数x“四舍五入”到个位的值记为![]() ,且值为3,进而得出x的取值范围;
,且值为3,进而得出x的取值范围;
(2)根据方程组得到x+y的值,再利用![]() 得出m的范围,从而根据题干中
得出m的范围,从而根据题干中![]() 的意义得出结果;
的意义得出结果;
(3)根据![]() 得出x的取值范围,据此求出
得出x的取值范围,据此求出![]() 中y的最小值;
中y的最小值;
(4)利用![]() ,设
,设![]() ,k为整数,得出关于k的不等关系求出即可.
,k为整数,得出关于k的不等关系求出即可.
解:(1)①由题意可得:![]() 3;
3;
②∵![]() ,
,
∴![]()
∴![]() ;
;
(2)∵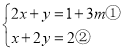 ,
,
①+②得:![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() =2;
=2;
(3)∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
当x=![]() 时,y最小,且为0;
时,y最小,且为0;
(4)设![]() ,k为整数,则
,k为整数,则![]() ,
,
∴![]() ,
,
∴![]() ,k≥0,
,k≥0,
∴![]() ,
,
∴k=0,1,
则x=0或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度
 (厘米)与燃烧时间
(厘米)与燃烧时间 (小时)之间的关系如图所示,其中乙蜡烛燃烧时
(小时)之间的关系如图所示,其中乙蜡烛燃烧时 与
与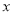 之间的函数关系式是
之间的函数关系式是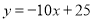 .
. 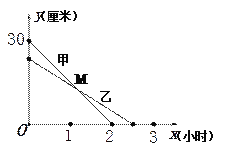
(1)甲蜡烛燃烧前的高度是_________厘米,乙蜡烛燃烧的时间是________小时.
(2)求甲蜡烛燃烧时
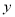 与
与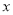 之间的函数关系式.
之间的函数关系式. (3)求出图中交点
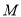 的坐标,并说明点
的坐标,并说明点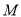 的实际意义.
的实际意义. -
科目: 来源: 题型:
查看答案和解析>>【题目】小赵为班级购买笔记本作为晚会上的奖品,回来时向生活委员交账说“一共买了36本,有两种规格,单价分别为1.8元和2.6元,去时我领了100元,现在找回27.6元.”生活委员算了一下,认为小赵稿错了.
(1)请你用方程的知识说明小赵为什么搞错了.
(2)小赵一想,发觉的确不对,因为他把自己口袋里的零用钱一起当做找回的钱给了生活委员,如果设购买单价为1.8元的笔记本
 本,并且小赵的零用钱数目是整数,且少于3元,试求出小赵零用钱的数目.
本,并且小赵的零用钱数目是整数,且少于3元,试求出小赵零用钱的数目. -
科目: 来源: 题型:
查看答案和解析>>【题目】一工地计划租用甲、乙两辆车清理淤泥,从运输量来估算:若租两车合运,10天可以完成任务;若单独租用乙车完成任务则比单独租用甲车完成任务多用15天.
(1)甲、乙两车单独完成任务分别需要多少天?
(2)已知两车合运共需租金65000元,甲车每天的租金比乙车每天的租金多1500元,试问:租甲乙两车、单独租甲车、单独租乙车这三种租车方案中,哪一种租金最少?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 经过
经过 顶点
顶点 的一条直线,
的一条直线, .
. 分别是直线
分别是直线 上两点,且
上两点,且 .
.(1)若直线
 经过
经过 的内部,且
的内部,且 在射线
在射线 上,请解决下面两个问题:
上,请解决下面两个问题:①如图1,若
 ,
, ,
,则
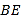
 ;
;
 (填“
(填“ ”,“
”,“ ”或“
”或“ ”);
”);②如图2,若
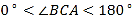 ,请添加一个关于
,请添加一个关于 与
与 关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.
关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.(2)如图3,若直线
 经过
经过 的外部,
的外部, ,请提出
,请提出 三条线段数量关系的合理猜想(不要求证明).
三条线段数量关系的合理猜想(不要求证明).
-
科目: 来源: 题型:
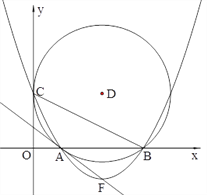
查看答案和解析>>【题目】如图24,在平面直角坐标系中,圆D与
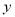 轴相切于点C(0,4),与
轴相切于点C(0,4),与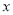 轴相交于A、B两点,且AB=6
轴相交于A、B两点,且AB=6(1)D点的坐标是 ,圆的半径为 ;
(2)求经过C、A、B三点的抛物线所对应的函数关系式;
(3)设抛物线的顶点为F,试证明直线AF与圆D相切;
(4)在
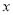 轴下方的抛物线上,是否存在一点N,使
轴下方的抛物线上,是否存在一点N,使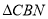 面积最大,最大面积是多少?并求出
面积最大,最大面积是多少?并求出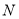 点坐标.
点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
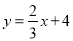 与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )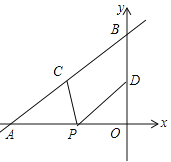
A.(﹣3,0) B.(﹣6,0) C.(
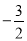 ,0) D.(
,0) D.( ,0)
,0)
相关试题

