【题目】![]() 经过
经过![]() 顶点
顶点![]() 的一条直线,
的一条直线,![]() .
.![]() 分别是直线
分别是直线![]() 上两点,且
上两点,且![]() .
.
(1)若直线![]() 经过
经过![]() 的内部,且
的内部,且![]() 在射线
在射线![]() 上,请解决下面两个问题:
上,请解决下面两个问题:
①如图1,若![]() ,
,![]() ,
,
则![]()
![]() ;
;![]()
![]() (填“
(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”);
”);
②如图2,若![]() ,请添加一个关于
,请添加一个关于![]() 与
与![]() 关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.
关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线![]() 经过
经过![]() 的外部,
的外部,![]() ,请提出
,请提出![]() 三条线段数量关系的合理猜想(不要求证明).
三条线段数量关系的合理猜想(不要求证明).
参考答案:
【答案】(1)①![]() ;
;![]() ;
;
②所填的条件是:![]() .
.
证明:在![]() 中,
中,![]() .
.
![]() ,
,![]() .
.
又![]() ,
,![]() .
.
又![]() ,
,![]() ,
,
![]() .
.
![]() ,
,![]() .
.
又![]() ,
,![]() .
.
(2)![]() .
.
【解析】
(1)①由∠BCA=90°,∠α=90°可得∠CBE+∠BCE=90°,∠BCE+∠ACD=90°,可推得∠CBE=∠ACD,且已知CA=CB,∠BEC=∠CFA,所以△BEC≌△CDA,可得BE=CF,EC=AF;又因为EF=CF-CE,所以EF=|BE-AF|;
②只有满足△BEC≌△CDA,才有①中的结论,即∠BCE=∠CAF,∠CBE=∠FCA;由三角形内角和等于180°,可知∠α+∠BCE+∠CBE=180°,即∠α+∠BCE+∠FCA=180°,即可得到∠α+∠BCA=180°.
(2)只要通过条件证明△BEC≌△CFA(可通过ASA证得),可得BE=CF,EC=AF,即可得到EF=EC+CF=BE+AF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小赵为班级购买笔记本作为晚会上的奖品,回来时向生活委员交账说“一共买了36本,有两种规格,单价分别为1.8元和2.6元,去时我领了100元,现在找回27.6元.”生活委员算了一下,认为小赵稿错了.
(1)请你用方程的知识说明小赵为什么搞错了.
(2)小赵一想,发觉的确不对,因为他把自己口袋里的零用钱一起当做找回的钱给了生活委员,如果设购买单价为1.8元的笔记本
 本,并且小赵的零用钱数目是整数,且少于3元,试求出小赵零用钱的数目.
本,并且小赵的零用钱数目是整数,且少于3元,试求出小赵零用钱的数目. -
科目: 来源: 题型:
查看答案和解析>>【题目】一工地计划租用甲、乙两辆车清理淤泥,从运输量来估算:若租两车合运,10天可以完成任务;若单独租用乙车完成任务则比单独租用甲车完成任务多用15天.
(1)甲、乙两车单独完成任务分别需要多少天?
(2)已知两车合运共需租金65000元,甲车每天的租金比乙车每天的租金多1500元,试问:租甲乙两车、单独租甲车、单独租乙车这三种租车方案中,哪一种租金最少?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】新定义:对非负数“四舍五入”到个位的值记为
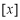 ,即当
,即当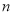 为非负整数时,若
为非负整数时,若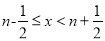 ,则
,则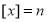 如:
如: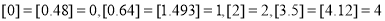 ,试解决下列问题
,试解决下列问题(1)填空:①
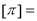 ②若
②若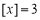 ,则实数
,则实数 的取值范围为
的取值范围为 (2)在关于
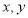 的方程组
的方程组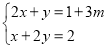 中,若未知数
中,若未知数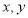 满足
满足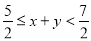 ,求
,求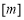 的值.
的值.(3)当
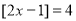 时,若
时,若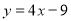 ,求
,求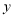 的最小值.
的最小值.(4)求满足
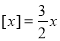 的所有非负实数
的所有非负实数 的值,请直接写出答案 .
的值,请直接写出答案 . -
科目: 来源: 题型:
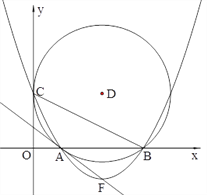
查看答案和解析>>【题目】如图24,在平面直角坐标系中,圆D与
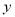 轴相切于点C(0,4),与
轴相切于点C(0,4),与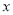 轴相交于A、B两点,且AB=6
轴相交于A、B两点,且AB=6(1)D点的坐标是 ,圆的半径为 ;
(2)求经过C、A、B三点的抛物线所对应的函数关系式;
(3)设抛物线的顶点为F,试证明直线AF与圆D相切;
(4)在
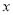 轴下方的抛物线上,是否存在一点N,使
轴下方的抛物线上,是否存在一点N,使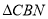 面积最大,最大面积是多少?并求出
面积最大,最大面积是多少?并求出 点坐标.
点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
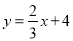 与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )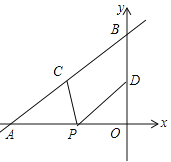
A.(﹣3,0) B.(﹣6,0) C.(
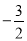 ,0) D.(
,0) D.( ,0)
,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (a是常数,a≠0),下列结论正确的是( )
(a是常数,a≠0),下列结论正确的是( )A.当a=1时,函数图象经过点(﹣1,1)
B.当a=﹣2时,函数图象与x轴没有交点
C.若a<0,函数图象的顶点始终在x轴的下方
D.若a>0,则当x≥1时,y随x的增大而增大
相关试题

