【题目】(2016·长沙中考)若抛物线L:y=ax2+x+c(a,b,c是常数,abc≠0)与直线l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与该抛物线L具有“一带一路”关系,此时,直线l叫作抛物线L的“带线”,抛物线L叫作直线l的“路线”.
(1)若直线y=mx+1与抛物线y=x2-2x+n具有“一带一路”关系,求m,n的值;
(2)若某“路线”L的顶点在反比例函数y=![]() 的图象上,它的“带线”l的解析式为y=2x-4,求此“路线”L的解析式.
的图象上,它的“带线”l的解析式为y=2x-4,求此“路线”L的解析式.
参考答案:
【答案】(1)m=-1,n=1;(2)y=2(x+1)2-6或y=-![]() (x-3)2+2.
(x-3)2+2.
【解析】试题分析: (1)令直线y=mx+1中x=0,则y=1,所以该直线与y轴的交点为(0,1),将(0,1)代入抛物线y=x2-2x+n中,得n=1,可求出抛物线的解析式为y=x2-2x+1=(x-1)2,所以抛物线的顶点坐标为(1,0).将点(1,0)代入到直线y=mx+1中,得0=m+1,解得m=-1,
(2)将y=2x-4和y=![]() 联立方程可得2x-4=
联立方程可得2x-4=![]() ,即2x2-4x-6=0,解得x1=-1,x2=3,所以该“路线”L的顶点坐标为(-1,-6)或(3,2),令“带线”l:y=2x-4中x=0,则y=-4,所以 “路线”L的图象过点(0,-4),设该“路线”L的解析式为y=m(x+1)2-6或y=n(x-3)2+2,由题意得:-4=m(0+1)2-6或-4=n(0-3)2+2,解得m=2,n=
,即2x2-4x-6=0,解得x1=-1,x2=3,所以该“路线”L的顶点坐标为(-1,-6)或(3,2),令“带线”l:y=2x-4中x=0,则y=-4,所以 “路线”L的图象过点(0,-4),设该“路线”L的解析式为y=m(x+1)2-6或y=n(x-3)2+2,由题意得:-4=m(0+1)2-6或-4=n(0-3)2+2,解得m=2,n=![]() ,所以此“路线”L的解析式为y=2(x+1)2-6或y=
,所以此“路线”L的解析式为y=2(x+1)2-6或y=![]() (x-3)2+2.
(x-3)2+2.
试题解析:(1)令直线y=mx+1中x=0,则y=1,即该直线与y轴的交点为(0,1),将(0,1)代入抛物线y=x2-2x+n中,得n=1,
∴抛物线的解析式为y=x2-2x+1=(x-1)2,
∴抛物线的顶点坐标为(1,0).将点(1,0)代入到直线y=mx+1中,得0=m+1,解得m=-1,
(2)将y=2x-4代入到y=![]() 中,得2x-4=
中,得2x-4=![]() ,即2x2-4x-6=0,解得x1=-1,x2=3,
,即2x2-4x-6=0,解得x1=-1,x2=3,
∴该“路线”L的顶点坐标为(-1,-6)或(3,2),
令“带线”l:y=2x-4中x=0,则y=-4,
∴“路线”L的图象过点(0,-4),
设该“路线”L的解析式为y=m(x+1)2-6或y=n(x-3)2+2,由题意得:
-4=m(0+1)2-6或-4=n(0-3)2+2,解得m=2,n=![]() ,
,
∴此“路线”L的解析式为y=2(x+1)2-6或y=![]() (x-3)2+2.
(x-3)2+2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断:
①OA=OC,②AB=CD,③∠BAD=∠DCB,④AD∥BC.
请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题:
(1)构造一个真命题,画图并给出证明;
(2)构造一个假命题,举反例加以说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线相交于点O,AC=2,BD=2
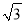 ,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为_____________
,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为_____________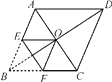
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数:
﹣3.1,3.1415,﹣
 ,+31,0.618,﹣
,+31,0.618,﹣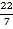 ,0,﹣1,﹣(﹣3),填在相应的集合里
,0,﹣1,﹣(﹣3),填在相应的集合里分数集合: ;
整数集合: ;
非负整数集合: ;
正有理数集合: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,
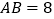 ,
,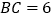 .将矩形ABCD沿过点C的直线折叠,使点B落在对角线AC上的点E处,折痕交AB于点F.
.将矩形ABCD沿过点C的直线折叠,使点B落在对角线AC上的点E处,折痕交AB于点F.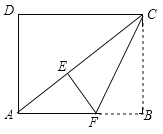
(1)求线段AC的长.
(2)求线段EF的长.
(3)点G在线段CF上,在边CD上存在点H,使以E、F、G、H为顶点的四边形是平行四边形,请画出
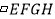 ,并直接写出线段DH的长.
,并直接写出线段DH的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:a是最大的负整数,b是最小的正整数,且c=a+b,请回答下列问题:

(1)请直接写出a,b,c的值:a= ;b= ;c= ;
(2)a,b,c在数轴上所对应的点分别为A,B,C,请在如图的数轴上表示出A,B,C三点;
(3)在(2)的情况下.点A,B,C开始在数轴上运动,若点A,点C以每秒1个单位的速度向左运动,同时,点B以每秒5个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,请问:AB﹣BC的值是否随着时间的变化而改变?若变化,请说明理由;若不变,请求出AB﹣BC的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点A、B、O在数轴上对应的数为a、b、0,且满足|a+8|+(b﹣12)2=0,点M、N分别从O、B出发,同时向左匀速运动,M的速度为1个单位长度每秒,N的速度为3个单位长度每秒,A、B之间的距离定义为:AB=|a﹣b|.
(1)直接写出OA= .OB= ;
(2)设运动的时间为t秒,当t为何值时,恰好有AN=2AM;
(3)若点P为线段AM的中点,Q为线段BN的中点,M、N在运动的过程中,PQ+MN的长度是否发生变化?若不变,请说明理由,若变化,当t为何值时,PQ+MN有最小值?最小值是多少?
相关试题

