【题目】已知:a是最大的负整数,b是最小的正整数,且c=a+b,请回答下列问题:
![]()
(1)请直接写出a,b,c的值:a= ;b= ;c= ;
(2)a,b,c在数轴上所对应的点分别为A,B,C,请在如图的数轴上表示出A,B,C三点;
(3)在(2)的情况下.点A,B,C开始在数轴上运动,若点A,点C以每秒1个单位的速度向左运动,同时,点B以每秒5个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,请问:AB﹣BC的值是否随着时间的变化而改变?若变化,请说明理由;若不变,请求出AB﹣BC的值.
参考答案:
【答案】(1)﹣1,1,0;(2)见解析;(3)AB﹣BC的值为1.
【解析】
(1)根据题意可得 (2)在数轴上直接标出.(3)先求出AB,BC的值,再计算AB-BC的值,可得AB-BC的值是定值.
(1)由题意可得a=﹣1,b=1,c=﹣1+1=0
(2)![]()
(3)∵BC=(1+5t)﹣(0﹣t)=1+6t,
AB=(1+5t)﹣(﹣1﹣t)=2+6t
∴AB﹣BC=2+6t﹣(1+6t)=1,
∴AB﹣BC的值不会随着时间的变化而改变,AB﹣BC的值为1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数:
﹣3.1,3.1415,﹣
 ,+31,0.618,﹣
,+31,0.618,﹣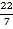 ,0,﹣1,﹣(﹣3),填在相应的集合里
,0,﹣1,﹣(﹣3),填在相应的集合里分数集合: ;
整数集合: ;
非负整数集合: ;
正有理数集合: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016·长沙中考)若抛物线L:y=ax2+x+c(a,b,c是常数,abc≠0)与直线l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与该抛物线L具有“一带一路”关系,此时,直线l叫作抛物线L的“带线”,抛物线L叫作直线l的“路线”.
(1)若直线y=mx+1与抛物线y=x2-2x+n具有“一带一路”关系,求m,n的值;
(2)若某“路线”L的顶点在反比例函数y=
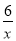 的图象上,它的“带线”l的解析式为y=2x-4,求此“路线”L的解析式.
的图象上,它的“带线”l的解析式为y=2x-4,求此“路线”L的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,
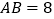 ,
,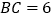 .将矩形ABCD沿过点C的直线折叠,使点B落在对角线AC上的点E处,折痕交AB于点F.
.将矩形ABCD沿过点C的直线折叠,使点B落在对角线AC上的点E处,折痕交AB于点F.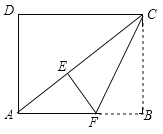
(1)求线段AC的长.
(2)求线段EF的长.
(3)点G在线段CF上,在边CD上存在点H,使以E、F、G、H为顶点的四边形是平行四边形,请画出
 ,并直接写出线段DH的长.
,并直接写出线段DH的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点A、B、O在数轴上对应的数为a、b、0,且满足|a+8|+(b﹣12)2=0,点M、N分别从O、B出发,同时向左匀速运动,M的速度为1个单位长度每秒,N的速度为3个单位长度每秒,A、B之间的距离定义为:AB=|a﹣b|.
(1)直接写出OA= .OB= ;
(2)设运动的时间为t秒,当t为何值时,恰好有AN=2AM;
(3)若点P为线段AM的中点,Q为线段BN的中点,M、N在运动的过程中,PQ+MN的长度是否发生变化?若不变,请说明理由,若变化,当t为何值时,PQ+MN有最小值?最小值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016广西桂林市)已知任意三角形的三边长,如何求三角形面积?
古希腊的几何学家海伦解决了这个问题,在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式S=
 (其中a,b,c是三角形的三边长,p=
(其中a,b,c是三角形的三边长,p= ,S为三角形的面积),并给出了证明
,S为三角形的面积),并给出了证明例如:在△ABC中,a=3,b=4,c=5,那么它的面积可以这样计算:
∵a=3,b=4,c=5,∴p=
 =6,∴S=
=6,∴S= =
= =6.
=6.事实上,对于已知三角形的三边长求三角形面积的问题,还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决.
如图,在△ABC中,BC=5,AC=6,AB=9
(1)用海伦公式求△ABC的面积;
(2)求△ABC的内切圆半径r.
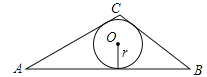
-
科目: 来源: 题型:
查看答案和解析>>【题目】大于1的正整数的三次方都可以分解为若干个连续奇数的和.如23=3+5,33=7+9+11,43=13+15+17+19.按此规律,若m3分解后,最后一个奇数为109,则m的值为______.
相关试题

