【题目】两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=1,固定△ABC不动,将△DEF进行如下操作: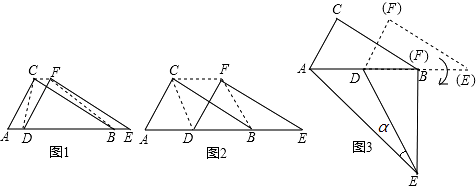
(1)操作发现
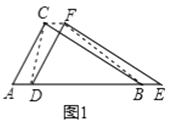
如图①,△DEF沿线段AB向右平移(即D点在线段AB内移动),连接DC、CF、FB,四边形CDBF的形状在不断变化,但它的面积不变化,请求出其面积.
(2)猜想论证
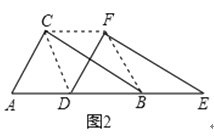
如图②,当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.
(3)拓展研究
如图③,△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB的边上,此时F点恰好与B点重合,连接AE,则sinα= .
参考答案:
【答案】
(1)解:如图1,∵△DEF沿线段AB向右平移(即D点在线段AB内移动),
∴CF=AD,AC=DF,
∴四边形ACFD为平行四边形,
∴AD∥CF,
∴S△DCF=S△BCF=S△ACD,
∴S四边形CDBF=S△CDB+S△BCF=S△CDB+S△ACD=S△ACB,
在Rt△ACB中,∵∠A=60°,
∴BC= ![]() AC=
AC= ![]() ,
,
∴S△ABC= ![]() ×1×
×1× ![]() =
= ![]() ,
,
∴S四边形CDBF= ![]()
(2)解:四边形CDBF为菱形.理由如下:
如图2,∵点D为斜边AB的中点,
∴DC=DA=DB,
∵CF∥AD,CF=AD,
∴CF=BD,CF∥DB,
∴四边形CDBF为平行四边形,
而DC=DB,
∴四边形CDBF为菱形;
(3)![]()
【解析】解:(3)作DH⊥AE于H,如图,
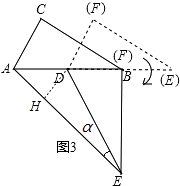
在Rt△ACB中,∵∠A=60°,
∴AB=2AC=2,
∵点D为AB的中点,
∴AD=BD= ![]() AB=1,
AB=1,
∵绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,
∴∠EFD=90°,EB= ![]() ,DE=AB=2,
,DE=AB=2,
在Rt△ABE中,AE= ![]() =
= ![]() =
= ![]() ,
,
∵ ![]() DHAB=
DHAB= ![]() ADEB,
ADEB,
∴DH= ![]() =
= ![]() ,
,
在Rt△EDH中,sinα= ![]() =
= ![]() .
.
所以答案是 ![]() .
.
【考点精析】掌握平移的性质和锐角三角函数的定义是解答本题的根本,需要知道①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等;锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究题.
用棋子摆成的“T”字形图如图所示:

(1)填写下表:
图形序号
①
②
③
④
…
⑩
每个图案中棋子个数
5
8
…
(2)写出第n个“T”字形图案中棋子的个数_________________(用含n的代数式表示);
(3)第20个“T”字形图案共有棋子____________个?
(4)计算前20个“T”字形图案中棋子的总个数.
(提示:请你先思考下列问题:第1个图案与第20个图案中共有多少个棋子?第2个图案与第19个图案中共有多少个棋子?第3个图案与第18个图案呢?)
-
科目: 来源: 题型:
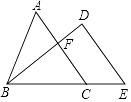
查看答案和解析>>【题目】如图,△ABC与△DBE中,AC∥DE,点B、C、E在同一直线上,AC,BD相交于点F,若∠BDE=85°,∠BAC=55°,∠ABD:∠DBE=3:4,求∠DBE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】新兴服装厂生产一种夹克和T恤,夹克每件定价
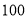 元,T恤每件定价
元,T恤每件定价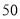 元.厂方在开展促销活动期间,向客户提供两种优惠方案:①买一件夹克送一件T恤;②夹克和T恤都按定价的
元.厂方在开展促销活动期间,向客户提供两种优惠方案:①买一件夹克送一件T恤;②夹克和T恤都按定价的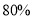 付款.现某客户要到该服装厂购买夹克
付款.现某客户要到该服装厂购买夹克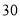 件,T恤
件,T恤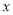 件(
件(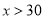 ).
).(1)若该客户按方案①购买,夹克需付款________元,T恤需付款________元(用含
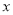 的式子表示);若该客户按方案②购买,夹克需付款______元,T恤需付款______元(用含
的式子表示);若该客户按方案②购买,夹克需付款______元,T恤需付款______元(用含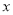 的式子表示);
的式子表示);(2)若
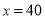 ,通过计算说明按方案①、方案②哪种方案购买较为合算?
,通过计算说明按方案①、方案②哪种方案购买较为合算? -
科目: 来源: 题型:
查看答案和解析>>【题目】一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完
 假设每分钟的进水量和出水量是两个常数,容器内的水量
假设每分钟的进水量和出水量是两个常数,容器内的水量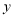 (单位:升)与时间
(单位:升)与时间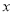 (单位:分钟)之间的部分关系如图象所示
(单位:分钟)之间的部分关系如图象所示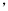 从开始进水到把水放完需要多少分钟.( )
从开始进水到把水放完需要多少分钟.( )
A.20B.24C.18D.16
-
科目: 来源: 题型:
查看答案和解析>>【题目】某检修小组乘一辆检修车沿一段东西方向铁路检修,规定向东走为正,向西走为负,小组的出发地记为M,某天检修完毕时,行走记录(单位:千米)如下:
+12,-5,-9,+10,-4,+15,-9,+3,-6,-3,-7
(1)问收工时,检修小组距出发地M有多远?在东侧还是西侧?
(2)若检修车每千米耗油0.2升,求从出发到收工时检修车共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了让更多的居民享受免费的体育健身服务,重庆市将陆续建成多个社区健身点,某社区为了了解健身点的使用情况,现随机调查了部分社区居民,将调查结果分成四类,A:每天健身;B:经常健身;C:偶尔健身;D:从不健身;并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图,解答下列问题:
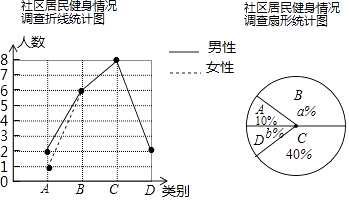
(1)本次调查中,一共调查了名社区居民,其中a=;请将折线统计图补充完整;
(2)为了吸引更多社区居民参加健身,健身点准备举办一次健身讲座培训,为此,想从被调查的A类和D类居民中分别选取一位在讲座上进行交流,请用列表法或画树状图的方法列出所有等可能的结果,并求出所选两位居民恰好是一位男性和一位女性的概率.
相关试题

